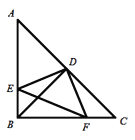
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D是AC的中点,直角
,点D是AC的中点,直角![]() 的两边分别交AB、BC于点E、F,给出以下结论:①
的两边分别交AB、BC于点E、F,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 是等腰直角三角形. 当
是等腰直角三角形. 当![]() 在
在![]() 内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.
内绕顶点D旋转时(点E不与点A、B重合),上述结论始终成立的有____________个.
参考答案:
【答案】4
【解析】
由ED垂直于FD,BD垂直于AC,利用同角的余角相等得到一对角相等,再由三角形ABC为等腰直角三角形得到BD=CD,且∠EBD=∠C=45°,利用ASA得到三角形BED与三角形CFD全等,利用全等三角形的对应边相等,对应角相等即可做出判断.
∵ED⊥FD,BD⊥AC,
∴∠BDE+∠BDF=90°,∠BDF+∠FDC=90°,
∴∠BDE=∠FDC,
∵B、E、D、F四点共圆,
∴∠BFE=∠BDE,
∴∠BFE=∠CDF,选项④正确;
∵△ABC为等腰直角三角形,BD⊥AC,
∴∠EBD=∠C=45°,BD=CD,
在△BED和△CFD中,
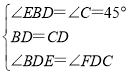 ,
,
∴△BED≌△CFD(ASA),
∴BE=CF,
∴AE=BF,选项①正确;
DE=DF,
∴△DEF为等腰直角三角形,选项⑤正确;
∴S四边形BEDF=S△BED+S△BDF=S△CFD+S△BDF=S△BDC=![]() S△ABC,选项②正确.
S△ABC,选项②正确.
∵BD是定值,EF随DF的变化而变化,只有当DF⊥BC时,EF=BD,
∴③不正确,
∴上述结论中始终成立的有4个.
故答案为:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程
 =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )A. 每天比原计划多铺设10米,结果延期20天完成
B. 每天比原计划少铺设10米,结果延期20天完成
C. 每天比原计划多铺设10米,结果提前20天完成
D. 每天比原计划少铺设10米,结果提前20天完成
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,点
,点 、
、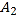 、
、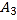 、…在射线ON上,点
、…在射线ON上,点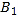 、
、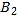 、
、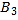 、…在射线OM上,
、…在射线OM上, 、
、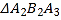 、
、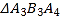 …均为等边三角形,若
…均为等边三角形,若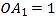 ,则
,则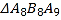 的边长为( )
的边长为( )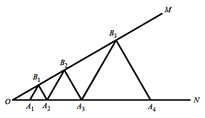
A.16B.64C.128D.256
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(
 ,y1),点N(
,y1),点N( ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣ <a<﹣
<a<﹣ .其中正确结论有( )
.其中正确结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
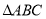 三个顶点的坐标分别为
三个顶点的坐标分别为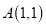 、
、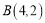 、
、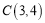 .
.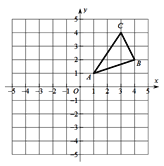
(1)若
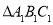 与
与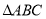 关于y轴成轴对称,则
关于y轴成轴对称,则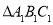 三个顶点坐标分别为
三个顶点坐标分别为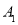 _________,
_________,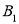 ____________,
____________,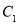 ____________;
____________;(2)若P为x轴上一点,则
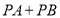 的最小值为____________;
的最小值为____________;(3)计算
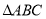 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①
 =﹣1;②ac+b+1=0;③abc>0;④a﹣b+c>0.其中正确的个数是( )
=﹣1;②ac+b+1=0;③abc>0;④a﹣b+c>0.其中正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线C1:y1=mx2﹣4mx+2n﹣1与平行于x轴的直线交于A、B两点,且A点坐标为(﹣1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,﹣1);③m>
 ;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是
;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是 ≤a<2;⑤不等式mx2﹣4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
≤a<2;⑤不等式mx2﹣4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )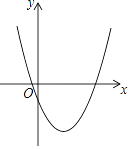
A. 2个 B. 3个 C. 4个 D. 5个
相关试题

