【题目】某开发公司生产的960件新产品需要精加工后才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲厂单独加工这批产品比乙工厂单独加工完这批产品多用20天,而甲工厂每天加工的数量是乙工厂每天加工数量的![]() ,甲、乙两个工厂每天各能加工多少个新产品?
,甲、乙两个工厂每天各能加工多少个新产品?
参考答案:
【答案】甲、乙两个工厂每天各能加工16个、24个新产品
【解析】
设乙每天加工新产品x件,则甲每天加工新产品![]() x件,甲单独加工完这批产品需
x件,甲单独加工完这批产品需![]() 天,乙单独加工完这批产品需
天,乙单独加工完这批产品需![]() 天,根据题意找出等量关系:甲厂单独加工这批产品所需天数-乙工厂单独加工完这批产品所需天数=20,由等量关系列出方程求解.
天,根据题意找出等量关系:甲厂单独加工这批产品所需天数-乙工厂单独加工完这批产品所需天数=20,由等量关系列出方程求解.
设乙每天加工新产品x件,则甲每天加工新产品![]() x件,
x件,
根据题意得![]()
![]() =20,
=20,
解得x=24,
经检验,x=24符合题意,
则![]() x=24×
x=24×![]() =16,
=16,
所以甲、乙两个工厂每天各能加工16个、24个新产品;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把平面内一条数轴
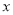 绕原点
绕原点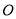 逆时针旋转角
逆时针旋转角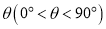 得到另一条数轴
得到另一条数轴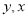 轴和
轴和 轴构成一个平面斜坐标系.过点
轴构成一个平面斜坐标系.过点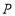 作
作 轴的平行线,交
轴的平行线,交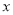 轴于点
轴于点 ,过点
,过点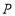 作
作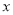 轴的平行线,交
轴的平行线,交 轴于点
轴于点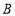 .若点
.若点 在
在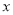 轴上对应的实数为
轴上对应的实数为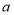 ,点
,点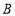 在
在 轴上对应的实数为
轴上对应的实数为 ,则成有序实数对
,则成有序实数对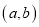 为点
为点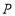 的斜坐标.
的斜坐标.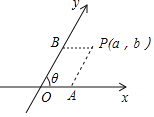
(1)在某平面斜坐标系中,已知
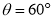 ,点
,点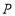 的斜坐标为
的斜坐标为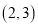 ,点
,点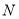 与点
与点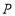 关于
关于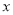 轴对称,求点
轴对称,求点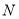 的斜坐标.
的斜坐标.(2)某平面斜坐标系中,已知点
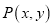 ,求出点
,求出点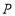 关于
关于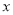 轴、
轴、 轴的对称点
轴的对称点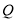 点、
点、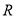 点的斜坐标.(用含
点的斜坐标.(用含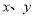 及
及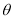 的式子表示).
的式子表示).(3)直接写出点
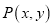 关于原点对称的点的斜坐标是_________.
关于原点对称的点的斜坐标是_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形
 的边
的边 的边分别在
的边分别在 轴,
轴, 轴正半轴上,
轴正半轴上, , 点
, 点 从点
从点 出发以每秒2个单位长度的速度向终点
出发以每秒2个单位长度的速度向终点 运动,点
运动,点 不与点
不与点 重合以
重合以 为边在
为边在 上方作正方形
上方作正方形 ,设正方形
,设正方形 与
与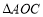 的重叠部分图形的面积为
的重叠部分图形的面积为 (平方单位),点
(平方单位),点 的运动时间为
的运动时间为 (秒).
(秒).
(1)直线
 所在直线的解析式是__________________________.
所在直线的解析式是__________________________.(2)当点
 落在线段
落在线段 上时,求
上时,求 的值.
的值.(3)在点
 运动的过程中,求
运动的过程中,求 与
与 之间的函数关系式;
之间的函数关系式;(4)设边
 的中点为
的中点为 ,点
,点 关于点
关于点 的对称点为
的对称点为 ,以
,以 为边在
为边在 上方作正方形
上方作正方形 当正方形
当正方形 与
与 重叠部分图形为三角形时,直接写出
重叠部分图形为三角形时,直接写出 的取值范围.
的取值范围.(提示:根据点
 的运动,可在草纸上画出正方形
的运动,可在草纸上画出正方形 与
与 重叠部分图形为不同图形时的临界状态去研究.)
重叠部分图形为不同图形时的临界状态去研究.) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
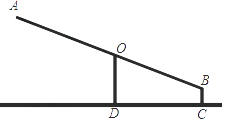
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
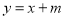 与双曲线
与双曲线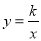 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.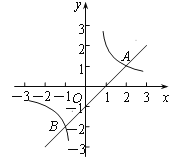
(1)求m及k的值;
(2)不解关于x、y的方程组
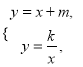 直接写出点B的坐标;
直接写出点B的坐标;(3)直线
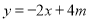 经过点B吗?请说明理由.
经过点B吗?请说明理由.【答案】(1)m=-1,k=2;(2)(-1,-2);(3)经过
【解析】试题分析:(1)把A(2,1)分别代入直线
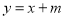 与双曲线
与双曲线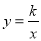 即可求得结果;
即可求得结果;(2)根据函数图象的特征写出两个图象的交点坐标即可;
(3)把x=-1,m=-1代入
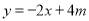 即可求得y的值,从而作出判断.
即可求得y的值,从而作出判断.(1)把A(2,1)分别代入直线
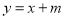 与双曲线
与双曲线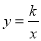 的解析式得m=-1,k=2;
的解析式得m=-1,k=2;(2)由题意得B的坐标(-1,-2);
(3)当x=-1,m=-1代入
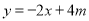 得y=-2×(-1)+4×(-1)=2-4=-2
得y=-2×(-1)+4×(-1)=2-4=-2所以直线
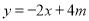 经过点B(-1,-2).
经过点B(-1,-2).考点:反比例函数的性质
点评:反比例函数的性质是初中数学的重点,是中考常见题,一般难度不大,需熟练掌握.
【题型】解答题
【结束】
20【题目】某气球内充满了一定质量的气球,当温度不变时,气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示(千帕是一种压强单位)
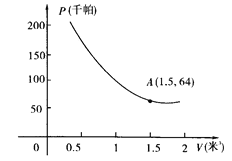
(1)写出这个函数的解析式;
(2)当气球的体积为0.8立方米时,气球内的气压是多少千帕;
(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米。
-
科目: 来源: 题型:
查看答案和解析>>【题目】位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)

-
科目: 来源: 题型:
查看答案和解析>>【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
相关试题

