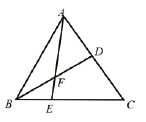
【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为![]() 且
且![]() =24,则
=24,则![]() =___________
=___________
参考答案:
【答案】4
【解析】分析: 利用三角形面积公式,等高的三角形的面积比等于底边的比,则S△AEC=![]() S△ABC=16,S△BCD=
S△ABC=16,S△BCD=![]() S△ABC=12,然后利用S△AEC-S△BCD=4即可得到答案.
S△ABC=12,然后利用S△AEC-S△BCD=4即可得到答案.
详解: :∵EC=2BE,
∴S△AEC=![]() S△ABC=
S△ABC=![]() ×24=16,
×24=16,
∵点D是AC的中点,
∴S△BCD=![]() S△ABC=
S△ABC=![]() ×24=12,
×24=12,
∴S△AEC-S△BCD=4,
即S△ADF+S四边形CEFD-(S△BEF-S四边形CEFD)=4,
∴S△ADF-S△BEF=4.
故答案为:4.
点睛: 本题考查了三角形面积:三角形的面积等于底边长与高线乘积的一半,即S△=![]() ×底×高;三角形的中线将三角形分成面积相等的两部分.
×底×高;三角形的中线将三角形分成面积相等的两部分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2
 ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
-
科目: 来源: 题型:
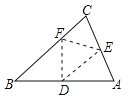
查看答案和解析>>【题目】折叠三角形纸片ABC,使点A落在BC边上的点F,且折痕DE∥BC,若∠A=75°,∠C=60°,则∠BDF=____________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】全等三角形的_____相等,_______相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个底角为 36°,那么顶角为____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的_____、_______、底边上的高互相重合.
-
科目: 来源: 题型:
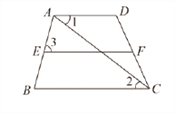
查看答案和解析>>【题目】已知:如图,∠D=110°,∠EFD=70°,∠1=∠2,求证:∠3=∠B
证明:
∵∠D=110°,∠EFD=70°(已知)
∴∠D+∠EFD=180°
∴AD∥EF( )
又∵∠1=∠2(已知)
∴ ∥ (内错角相等,两直线平行)
∴EF∥BC( )
∴∠3=∠B( )
相关试题

