【题目】已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F. 当BE=CF时,求证:AE=AF.

参考答案:
【答案】证明过程见解析
【解析】
试题分析:过点B作BG∥FC,延长FD交BG于点G,证明△BDG和△CDF全等,得到BG=CF,然后根据BE=CF,从而说明△BEG为等腰三角形,即∠G=∠BEG,根据平行可得∠G=∠F,根据对顶角可得∠BEG=∠AEF,根据等式的性质可得∠F=AEF,从而得出AE=AF.
试题解析:过点B作BG∥FC,延长FD交BG于点G.∴![]() .
.
∵点D是BC的中点,∴BD=CD.
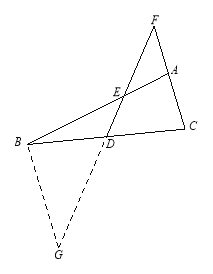
在△BDG和△CDF中,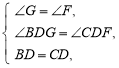
∴ △BDG≌△CDF. ∴BG=CF. ∵BE=CF, ∴BE=BG.
∴∠G=∠BEG ∵∠BEG=∠AEF ∴∠G=∠AEF ∴∠F=∠AEF ∴AE=AF
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数是
①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简:
(1)2(a 4)3+a14÷a2—a2·a10 (2)(—2009)0+(
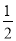 )—1+(—2)3
)—1+(—2)3(3)(x-1)2+(2x+5)(5-2x) (4)(a+3b-2c)(a-3b-2c)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,某客运公司的甲、乙两辆客车分别从相距380千米的A、B两地同时出发相向而行,并以各自的速度匀速行驶,两车行驶2小时时甲车先到达服务区C地,此时两车相距20千米,甲车在服务区C地休息了20分钟,然后按原速度开往B地;乙车行驶2小时15分钟时也经过C地,未停留继续开往A地.(友情提醒:画出线段图帮助分析)
(1)乙车的速度是 千米/小时,B、C两地的距离是 千米, A、C两地的距离是 千米;
(2)求甲车的速度;
(3)这一天,乙车出发多长时间,两车相距200千米?
-
科目: 来源: 题型:
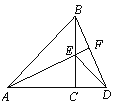
查看答案和解析>>【题目】如图,△ACB和△ECD都是等腰直角三角形,A、C、D三点在同一直线上,连接BD、AE,并延长AE交BD于F。
(1)求证:△ACE≌△BCD;
(2)直线AE与BD互相垂直吗?请证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣3+2=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等式x2·x3·( )=x12中,括号里面应填( )
A. x2 B. x6 C. x7 D. x8
相关试题

