【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的长为_____.

参考答案:
【答案】![]()
【解析】分析:根据三角形中位线定理得MN=![]() AD,根据直角三角形斜边中线定理得BM=
AD,根据直角三角形斜边中线定理得BM=![]() AC,从而可证MN=BM,;再由∠BMN=90°,根据BN2=BM2+MN2即可解决问题.
AC,从而可证MN=BM,;再由∠BMN=90°,根据BN2=BM2+MN2即可解决问题.
详解:在△CAD中,∵M、N分别是AC、CD的中点,
∴MN∥AD,MN=![]() AD,
AD,
在Rt△ABC中,∵M是AC中点,
∴BM=![]() AC,
AC,
∵AC=AD,
∴MN=BM,
∵∠BAD=60°,AC平分∠BAD,
∴∠BAC=∠DAC=30°,
∴BM=![]() AC=AM=MC,
AC=AM=MC,
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,
∵MN∥AD,
∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°,
∴BN2=BM2+MN2,
∴MN=BM=![]() AC=1,
AC=1,
∴BN=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处。
(1)求证:四边形AECF是平行四边形;
(2)若AB=6,AC=10,求四边形AECF的面积。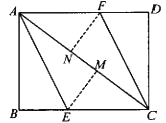
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两船从同一个港口同时出发反向而行,甲船顺水航行了6小时,乙船逆水行了3小时,两船在静水中的速度都是50 km/h,水流速度是a km/h
(1) 两船一共航行了多少千米
(2) 甲船比乙船多航行多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣
 与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.
与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.(1)求抛物线的函数表达式;
(2)若点D在第二象限且满足CD=5AC,求此时直线1的解析式;在此条件下,点E为直线1下方抛物线上的一点,求△ACE面积的最大值,并求出此时点E的坐标;
(3)如图,设P在抛物线的对称轴上,且在第二象限,到x轴的距离为4,点Q在抛物线上,若以点A,D,P,Q为顶点的四边形能否成为平行四边形?若能,请直接写出点Q的坐标;若不能,请说明理由.

-
科目: 来源: 题型:
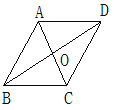
查看答案和解析>>【题目】在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是48cm.求:
(1)两条对角线的长度;(2)菱形的面积.
-
科目: 来源: 题型:
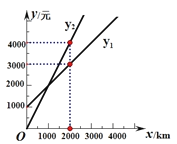
查看答案和解析>>【题目】某单位急需用车,但不准备买车,他们准备和一个体车主或一国营出租车公司中的一家签订合同,设汽车每月行驶x km,应付给个体车主的月租费是y1元,应付给国营出租车公司的月租费是y2元, y1, y2分别与x之间的函数关系的图象(两条射线)如图所示,观察图象,回答下列问题.
(1)分别写出y1, y2与x之间的函数关系式;
(2)每月行驶的路程在什么范围内时,租国营公司的车合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:
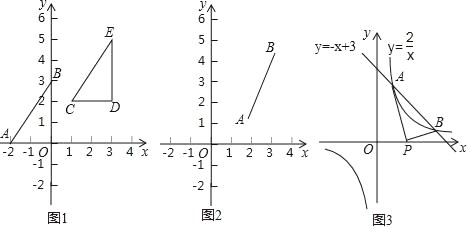
(1)图1中,已知线段AB,A(﹣2,0),B(0,3),则线段AO的长为2,BO的长为3,所以线段AB的长为;把Rt△AOB向右平移3个单位,再向上平移2个单位,得到Rt△CDE.
则Rt△CDE的顶点坐标分别为C(1,2),D(3,2),E(3,5);此时线段CD的长为 ,DE的长为 ,所以线段CE的长为 .
(2)在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB的长AB= (用含a,b,c,d的代数式表示,写出推导过程);
归纳:无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(a,b),B(c,d)时,线段AB的长为AB= .(不必证明)
(3)运用 在图3中,一次函数y=﹣x+3与反比例函数y=
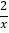 的图象交点为A,B.
的图象交点为A,B.①求出交点A、B的坐标;
②线段AB的长;
③点P是x轴上动点,求PA+PB的最小值.
相关试题

