搜索
【题目】如图，要判定AB∥CD，需要哪些条件？根据是什么？
参考答案：
【答案】①∠D＋∠DAB＝180°，根据是同旁内角互补，两直线平行． ②∠CEA＋∠EAB＝180°，根据是同旁内角互补，两直线平行或∠DEA＝∠EAB，根据是内错角相等，两直线平行．③∠DCA＝∠CAB，根据是内错角相等，两直线平行． ④则需∠DCF＋∠AFC＝180°，根据是同旁内角互补，两直线平行或∠DCF＝∠BFC，根据是内错角相等，两直线平行． ⑤∠DCB＋∠B＝180°，根据是同旁内角互补，两直线平行．
【解析】
根据内错角相等，两直线平行找条件判定AB∥CD；根据同旁内角互补，两直线平行找条件判定AB∥CD．
①若考虑截线AD，则需∠D＋∠DAB=180°，根据是同旁内角互补，两直线平行．
②若考虑截线AE，则需∠CEA＋∠EAB=180°，根据是同旁内角互补，两直线平行或∠DEA=∠EAB，根据是内错角相等，两直线平行．
③若考虑截线AC，则需∠DCA=∠CAB，根据是内错角相等，两直线平行．
④若考虑截线FC，则需∠DCF＋∠AFC=180°，根据是同旁内角互补，两直线平行或∠DCF=∠BFC，根据是内错角相等，两直线平行．
⑤若考虑截线BC，则需∠DCB＋∠B=180°，根据是同旁内角互补，两直线平行．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB∥CD，EF分别交AB、CD于G、F两点，射线FM平分∠EFD，将射线FM平移，使得端点F与点G重合且得到射线GN．若∠EFC=110°，则∠AGN的度数是（ ）
A. 120° B. 125° C. 135° D. 145°
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的方程x2﹣2（k﹣1）x+k2=0有两个实数根x1 ， x2 ．
（1）求k的取值范围；
（2）若|x1+x2|=x1x2﹣1，求k的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】陆老师布置了一道题目：过直线l外一点A作l的垂线．（用尺规作图）
小淇同学作法如下：
（1）在直线l上任意取一点C，连接AC；
（2）作AC的中点O；
（3）以O为圆心，OA长为半径画弧交直线l于点B，如图所示；
（4）作直线AB．
则直线AB就是所要作图形．
你认为小淇的作法正确吗？如果不正确，请画出一个反例；如果正确，请给出证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，点P是直线l3上一动点
（1）如图1，当点P在线段CD上运动时，∠PAC，∠APB，∠PBD之间存在什么数量关系？请你猜想结论并说明理由．
（2）当点P在C、D两点的外侧运动时（P点
与点C、D不重合，如图2和图3），上述（1）中的结论是否还成立？若不成立，请直接写出∠PAC，∠APB，∠PBD之间的数量关系，不必写理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（定义）数学课上，陈老师对我们说，如果1条线段将一个三角形分成2个等腰三角形，那么这1条线段就称为这个三角形的“好线”，如果2条线段将一个三角形分成3个等腰三角形，那么这2条线段就称为这个三角形的“好好线”．
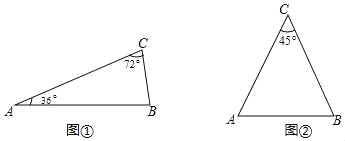
（理解）如图①，在△ABC中，∠A＝36°，∠C＝72°，请你在这个三角形中画出它的“好线”，并标出等腰三角形顶角的度数．
如图②，已知△ABC是一个顶角为45°的等腰三角形，请你在这个三角形中画出它的“好好线”，并标出所分得的等腰三角形底角的度数．
（应用）
(1)在△ABC中，已知一个内角为42°，若它只有“好线”，请你写出这个三角形最大内角的所有可能值______；
(2)在△ABC中，∠C＝27°，AD和DE分别是△ABC的“好好线”，点D在BC边上，点E在AB边上，且AD＝DC，BE＝DE，请你根据题意画出示意图，并求∠B的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB∥CD，EF分别交AB、CD于G、F两点，射线FM平分∠EFD，将射线FM平移，使得端点F与点G重合且得到射线GN．若∠EFC=110°，则∠AGN的度数是（ ）
A. 120° B. 125° C. 135° D. 145°
相关试题
