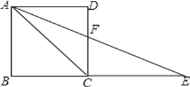
【题目】如图所示,E为正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,那么∠AFC的度数为( )
A. 112.5° B. 125° C. 135° D. 150°
参考答案:
【答案】A
【解析】
根据等边对等角的性质可得∠E=∠CAE,然后根据正方形的对角线平分一组对角以及三角形的一个外角等于与它不相邻的两个内角的和列式求出∠E=22.5°,再根据 三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解:∵CE=AC,
∴∠E=∠CAE,
∵AC是正方形ABCD的对角线,
∴∠ACB=45°,
∴∠E+∠CAE=45°,
∴∠E=![]() ×45°=22.5°,
×45°=22.5°,
在△CEF中,∠AFC=∠E+∠ECF=22.5°+90°=112.5°.
故答案为:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是 _____________ ,(证明你的结论. )
(2)当四边形ABCD的对角线满足 __________条件时,四边形EFGH是矩形(不用证明)

-
科目: 来源: 题型:
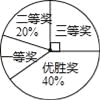
查看答案和解析>>【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
(1)当t为何值时,四边形PODB是平行四边形?
(2)△OPD为等腰三角形时,写出点P的坐标(请直接写出答案,不必写过程).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为

A.
 B. 5C. 3D.
B. 5C. 3D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
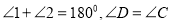 ,求证:
,求证: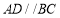 ,请将证明过程填写完整.
,请将证明过程填写完整.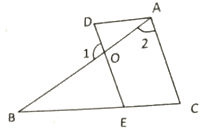
证明:∵
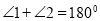 (已知)
(已知)又∵
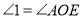 ( )
( )∴________
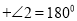 ,
,∴
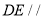 ____________( )
____________( )∴
 ______________( )
______________( )又∵
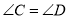 (已知)
(已知)∴
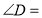 ________________,
________________,∴
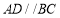 ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:我们把对角线相等的四边形叫做和美四边形.
 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子. 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形; 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O, ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
相关试题

