【题目】在数轴上,A点表示2,现在点A向右移动两个单位后到达点B;再向左移动10个单位到达C点:
(1)请在数轴上表示出A点开始移动时位置及B、C点位置;
(2)当A点移动到C点时,若要再移动到原点,问必须向哪个方向移动多少个单位?
(3)请把A点从开始移动直至到达原点这一过程,用一个有理数算式表达出来.
参考答案:
【答案】(1)见详解;(2)向右移动6个单位;(3)0.
【解析】
运用数轴上坐标的特点,向左移动用减法,向右移动用加法求解即可.
(1)如图,
![]()
(2)必须向右移动6个单位,移动到原点,
(3)根据数轴上坐标的特点,向左移动用减法,向右移动用加法,本题中A点为2,向右移动2个单位是+2,再向左移动10个单位,是10,这时候点A在6上,想到达6需要向右再移动6个单位;2+210+6=0.
试题根据数轴上坐标的特点,向左移动用减法,向右移动用加法,本题中A点为2,向右移动2个单位是+2,再向左移动10个单位,是-10,这时候点A在-6上,想到达-6需要向右再移动6个单位; 2+2-10+6=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB=2,点P是线段AB上一点,分别以AP、BP为边作两个正方形.

(1)如果APx,求两个正方形的面积之和S;
(2)当点P是AB的中点时,求两个正方形的面积之和S1;
(3)当点P不是AB的中点时,比较(1)中的S与(2)中S1的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有A型、B型、C型三种不同的纸板,其中A型:边长为a厘米的正方形;B型:长为a厘米,宽为1厘米的长方形;C型:边长为1厘米的正方形.
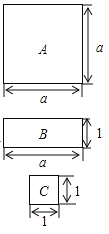
(1)A型2块,B型4块,C型4块,此时纸板的总面积为 平方厘米;
①从这10块纸板中拿掉1块A型纸板,剩下的纸板在不重叠的情况下,可以紧密的排出一个大正方形,这个大正方形的边长为 厘米;
②从这10块纸板中拿掉2块同类型的纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出两个相同的大正方形,请问拿掉的是2块哪种类型的纸板?(计算说明)
(2)A型12块,B型12块,C型4块,从这28块纸板中拿掉1块纸板,使得剩下的纸板在不重叠的情况下,可以紧密地排出三个相同形状的大正方形,则大正方形的边长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】前年,某大型工业企业落户万州,相关建设随即展开.到去年年底,工程进入到设备安装阶段.在该企业的采购计划中,有A、B、C三种生产设备.若购进3套A,7套B,1套丙,需资金63万元;若购进4套A,10套B,1套丙,需资金84万元.现在打算同时购进A、B、C各10套,共需资金___________________万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A,B,C是x轴的正半轴上从左向右依次排列的三点,过点A,B,C分别作与
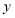 轴平行的直线
轴平行的直线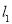 ,
,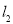 ,
, .
.
(1)如图1,若直线
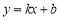 与直线
与直线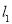 ,
,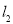 ,
, 分别交于点D,E,F三点,设D(
分别交于点D,E,F三点,设D(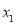 ,
,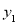 ),E(
),E(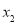 ,
,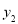 ),F(
),F(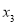 ,
,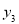 ) .
) .①若
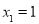 ,
,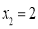 ,
,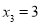 ,则
,则
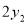 (填“=”,“>”或“<”);
(填“=”,“>”或“<”);②若
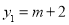 ,
,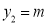 ,
,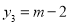 (
(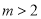 ),求证:AB=BC;
),求证:AB=BC;(2)如图2,点A,B,C的横坐标分别为
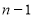 ,n,
,n, (
(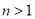 ),直线
),直线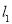 ,
,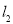 ,
, 与反比例函数
与反比例函数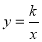 (
(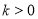 )的图像分别交于点D,E,F,根据以上探究的经验,探索
)的图像分别交于点D,E,F,根据以上探究的经验,探索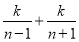 与
与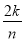 之间的大小关系,并说明理由.
之间的大小关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】能判定四边形
 是平行四边形的是( )
是平行四边形的是( )A.AB∥CD,
 B. AB∥CD,
B. AB∥CD,
C.
 ,
,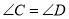 D.
D. ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并用相关的思想方法解决问题.
计算:(1﹣
 ﹣
﹣ ﹣
﹣ )×(
)×( +
+ +
+ )﹣(1﹣
)﹣(1﹣ ﹣
﹣ ﹣
﹣ )×(
)×( +
+ +
+ ).
).令
 +
+ +
+ =t,则原式=(1﹣t)(t+
=t,则原式=(1﹣t)(t+ )﹣(1﹣t﹣
)﹣(1﹣t﹣ )t=t+
)t=t+ ﹣t2﹣
﹣t2﹣ t﹣
t﹣ t+t2=
t+t2= ,
,问题:
(1)计算:(1﹣
 ﹣
﹣ ﹣
﹣ )×(
)×( +
+ +
+ )﹣(1﹣
)﹣(1﹣ ﹣
﹣ ﹣
﹣ )×(
)×( +
+ +
+ );
);(2)解方程(x2+5x+1)(x2+5x+7)=7.
相关试题

