【题目】已知:关于x的方程![]() ,
,
(1)求证:无论k取任何实数值,方程总有实数根;
(2)若等腰三角形ABC的一边长a=1,两个边长b,c恰好是这个方程的两个根,求△ABC的周长.
参考答案:
【答案】(1)证明见解析;(2)△ABC的周长为5.
【解析】
(1)根据一元二次方程根与判别式的关系即可得答案;
(2)分a为底边和a为腰两种情况,当a为底边时,b=c,可得方程的判别式△=0,可求出k值,解方程可求出b、c的值;当a为一腰时,则方程有一根为1,代入可求出k值,解方程可求出b、c的值,根据三角形的三边关系判断是否构成三角形,进而可求出周长.
(1)∵判别式△=[-(k+2)]-4×2k=k-4k+4=(k-2)≥0,
∴无论k取任何实数值,方程总有实数根.
(2)当a=1为底边时,则b=c,
∴△=(k-2)=0,
解得:k=2,
∴方程为x2-4x+4=0,
解得:x1=x2=2,即b=c=2,
∵1、2、2可以构成三角形,
∴△ABC的周长为:1+2+2=5.
当a=1为一腰时,则方程有一个根为1,
∴1-(k+2)+2k=0,
解得:k=1,
∴方程为x2-3x+2=0,
解得:x1=1,x2=2,
∵1+1=2,
∴1、1、2不能构成三角形,
综上所述:△ABC的周长为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(
 )-(
)-( );
);(2)
 ;
;(3)(2x+1)(x-1)=4;
(4)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,对角线
中,对角线 和
和 交于点
交于点 ,且点
,且点 是
是 和
和 的中点,若
的中点,若 的长为10,则
的长为10,则 和
和 的长可以是( )
的长可以是( )
A. 5和10B. 8和12C. 10和20D. 20和40
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, 和
和 分别平分
分别平分 和
和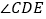 ,
, ,则
,则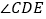 的度数为( )
的度数为( )
A. 16°B. 32°C. 48°D. 64°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=DC,AD=BC,E,F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= ( )

A. 150° B. 40° C. 80° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 ,把
,把 的直角三角板
的直角三角板 的直角顶点
的直角顶点 放在直线
放在直线 上.将直角三角板
上.将直角三角板 在平面内绕点
在平面内绕点 任意转动,若转动的过程中,直线
任意转动,若转动的过程中,直线 与直线
与直线 的夹角为60°,则
的夹角为60°,则 的度数为___.
的度数为___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A.
 B. 2 C.
B. 2 C.  D. 2
D. 2
相关试题

