【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,![]() 求
求![]() 长(结果保留π).
长(结果保留π).

参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OD,由切线的性质即可得出∠ODF=90°,再由BD=CD,OA=OB可得出OD是△ABC的中位线,根据三角形中位线的性质即可得出,根据平行线的性质即可得出∠CFD=∠ODF=90°,从而证出DF⊥AC;
(2)由∠CDF=30°以及∠ODF=90°即可算出∠ODB=60°,再结合OB=OD可得出△OBD是等边三角形,根据弧长公式即可得出结论.
试题解析:(1)证明:连接OD,如图所示.
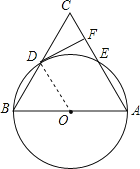
∵DF是⊙O的切线,D为切点,
∴OD⊥DF,
∴∠ODF=90°
∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC,
∴∠CFD=∠ODF=90°,
∴DF⊥AC.
(2)解:∵∠CDF=30°,
由(1)得∠ODF=90°,
∴∠ODB=180°-∠CDF-∠ODF=60°
∵OB=OD,
∴△OBD是等边三角形,
∴∠BOD=60°,
∴BD弧的长= ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图 题(要求:尺规作图,不写作法,保留作图痕迹)如图,平面上有三个村庄A、B、C,现计划打一水井P,使水井P到三个村庄的距离相等.
(1)请你在图中画出水井P的位置;
(2)若∠BAC=120°,BC=
 米,求PA的长.
米,求PA的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=2时,代数式ax﹣2的值是4;那么,当x=﹣2时,这代数式的值是( )
A.﹣4
B.﹣8
C.8
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.
(1)求证:△DFB是等腰三角形;
(2)若DA=
 AF,求证:CF⊥AB.
AF,求证:CF⊥AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x﹣y=a,xy=a+3,且x2+y2=5,则a的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
(1)解方程:
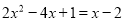
解:方程化为:
 .
.即化为:(2x-3)(x-1)=0,
∴ 2x-3=0或x-1=0,
解得:x=
 或x=1.
或x=1.∴方程的根为:
 ,
,  .
.(2)求解分式方程的过程是:将分式方程化为整式方程,然后求解整式方程,然后将整工方程的根代入验根,舍去增根,得到的根就是原方程的根.
参考上述材料,解决下列问题:
(1)解方程:
 ;
;(2)若方程
 的一个解是x=1,则方程的其他解是__________.
的一个解是x=1,则方程的其他解是__________.
相关试题

