【题目】已知x2+mx+25是完全平方式,则m= .
参考答案:
【答案】±10
【解析】解:∵x2+mx+25=x2+mx+52是完全平方式,
∴m=±2×5=±10.
所以答案是:±10.
【考点精析】本题主要考查了完全平方公式的相关知识点,需要掌握首平方又末平方,二倍首末在中央.和的平方加再加,先减后加差平方才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,ABCD中,E、F分别是边AB、CD的中点.
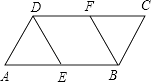
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
2013年,北京发布《2013年至2017年清洁空气行动计划》,北京的空气污染治理目标是力争到2017年全市PM2.5年均浓度比2012年下降25%以上,控制在60微克/立方米左右.
根据某空气监测单位发布数据,2013年北京PM2.5年均浓度89.5微克/立方米,清洁空气问题引起了所有人的高度关注.2014年北京PM2.5年均浓度85.9微克/立方米,比2013年下降3.6微克/立方米.2015年北京PM2.5年均浓度80.6微克/立方米,比上一年又下降了5.3微克/立方米,治理成效比较明显. 2016年北京PM2.5年均浓度73微克/立方米,下降更加明显.
去年11月,北京市通过的《北京市“十三五”时期环境保护和生态环境建设规划》确定的生态环保目标为:2020年,北京市PM2.5年均浓度比2015年下降30%,全市空气质量优良天数比例超过56%.
根据以上材料解答下列问题: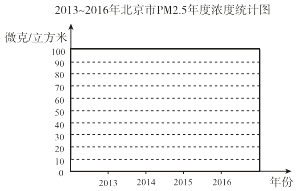
(1)在折线图中表示2013﹣2016年北京市PM2.5年度浓度变化情况,并在图中标明相应数据;
(2)根据绘制的折线图中提供的信息,预估2017年北京市PM2.5年均浓度为 , 你的预估理由是 .
(3)根据《北京市“十三五”时期环境保护和生态环境建设规划》,估计2020年北京市PM2.5年度浓度降至微克/每立方米.(结果保留整数) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,DE∥CA,∠1=∠2,∠3=∠4,∠BAC=84°.求∠EDA的度数.
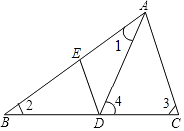
-
科目: 来源: 题型:
查看答案和解析>>【题目】现用棱长为1cm的若干小立方体,按如图所示的规律在地上搭建若个几何体.图中每个几何体自上而下分别叫第一层,第二层…第n层(n为正整数),其中第一层摆放一个小立方体,第二层摆放4个小立方体,第三层摆放9个小立方体…,依次按此规律继续摆放.
(1)求搭建第4个几何体需要的小立方体个数;
(2)为了美观,若将每个几何体的所有露出部分(不包含底面)都喷涂油漆,已知喷涂1cm2需要油漆0.2g.
①求喷涂第4个几何体需要油漆多少g?
②求喷涂第n个几何体需要油漆多少g?(用含n的代数式表示)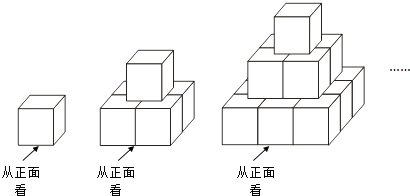
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:

(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“丹棱冻粑”是眉山著名特色小吃,产品畅销省内外,现有一个产品销售点在经销时发现:如果每箱产品盈利10元,每天可售出50箱;若每箱产品涨价1元,日销售量将减少2箱.
(1)现该销售点每天盈利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元才能获利最高?
相关试题

