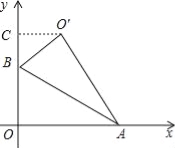
【题目】如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为(![]() ,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .

参考答案:
【答案】(![]() ,
,![]() )
)
【解析】
试题分析:作O′C⊥y轴于点C,首先根据点A,B的坐标分别为(![]() ,0),(0,1)得到∠BAO=30°,从而得出∠OBA=60°,然后根据Rt△AOB沿着AB对折得到Rt△AO′B,得到∠CBO′=60°,最后设BC=x,则OC′=
,0),(0,1)得到∠BAO=30°,从而得出∠OBA=60°,然后根据Rt△AOB沿着AB对折得到Rt△AO′B,得到∠CBO′=60°,最后设BC=x,则OC′=![]() x,利用勾股定理求得x的值即可求解.如图,作O′C⊥y轴于点C,
x,利用勾股定理求得x的值即可求解.如图,作O′C⊥y轴于点C,
∵点A,B的坐标分别为(![]() ,0),(0,1),∴OB=1,OA=
,0),(0,1),∴OB=1,OA=![]() ,∴tan∠BAO=
,∴tan∠BAO=![]() =
=![]() ,
,
∴∠BAO=30°,∴∠OBA=60°,∵Rt△AOB沿着AB对折得到Rt△AO′B,∴∠CBO′=60°,
∴设BC=x,则O′C=![]() x,∴x2+(
x,∴x2+(![]() x)2=1,解得:x=
x)2=1,解得:x=![]() (负值舍去),所以O′C=
(负值舍去),所以O′C=![]()
∴OC=OB+BC=1+![]() =
=![]() ,∴点O′的坐标为(
,∴点O′的坐标为(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. 四边都相等的四边形是平行四边形
B. 两组对角分别相等的四边形是平行四边形
C. 对角线互相垂直的四边形是平行四边形
D. 两组对边分别平行的四边形是平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,老师测量跳远成绩的主要依据是( )
A. 垂线段最短 B. 两点之间,线段最短
C. 平行线间的距离相等 D. 两点确定一条直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,已知A(0,a),B(b,b),C(c,a),其中a,b满足关系式|a-4|+ (b-2)2=0,c=a+b.
(1)求A、B、C三点的坐标,并在坐标系中画出△ABC;
(2)如果在第四象限内有一点P(2,m),请用含m的代数式表示三角形CPO的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】∠1与∠2互余,∠1与∠3互补,若∠3=125°,则∠2= ________度。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)当k=1时,求原方程的解.
(2)求证:无论k取任何实数时,方程总有实数根.
-
科目: 来源: 题型:
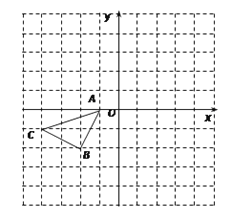
查看答案和解析>>【题目】如图所示的正方形网格中,△ABC 的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点P. 若点P向右平移x个单位长度后落在△A2B2C2的内部(不含落在△A2B2C2的边上),请直接写出x的取值范围.
(提醒:每个小正方形边长为1个单位长度)
相关试题

