【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)当k=1时,求原方程的解.
(2)求证:无论k取任何实数时,方程总有实数根.
参考答案:
【答案】(1)x1=-1 x2=-2;(2)见解析
【解析】试题分析:(1)把k=1代入方程中,解方程即可;
(2)分k=0,为一元一次方程;k≠0,利用根的判别式整理得出答案即可.
试题解析:
(1)把k=1代入kx2+(2k+1)x+2=0中得
x2+3x+2=0
(x+1)(x+2)=0
x1=-1 x2=-2;
(2)证明:∵当k=0,为x+2=0一元一次方程,解为x=-2;
当k≠0,△=(2k+1)2-4k×2=(2k-1)2≥0,
∴无论k取任何实数时,方程总有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,已知A(0,a),B(b,b),C(c,a),其中a,b满足关系式|a-4|+ (b-2)2=0,c=a+b.
(1)求A、B、C三点的坐标,并在坐标系中画出△ABC;
(2)如果在第四象限内有一点P(2,m),请用含m的代数式表示三角形CPO的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为(
 ,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】∠1与∠2互余,∠1与∠3互补,若∠3=125°,则∠2= ________度。
-
科目: 来源: 题型:
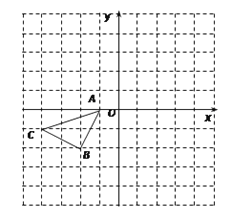
查看答案和解析>>【题目】如图所示的正方形网格中,△ABC 的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3)作出点C关于x轴的对称点P. 若点P向右平移x个单位长度后落在△A2B2C2的内部(不含落在△A2B2C2的边上),请直接写出x的取值范围.
(提醒:每个小正方形边长为1个单位长度)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a4÷a3=1 B. a4+a3=a7 C. (2a3 )4=8a12 D. a4a3=a7
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
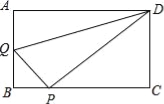

(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
相关试题

