练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

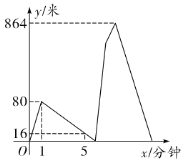
    【题目】疫情之下，中华儿女共抗时艰．重庆和湖北同饮长江水，为更好地驰援武汉，打赢防疫攻坚战，我市某公益组织收集社会捐献物资．甲、乙两人先后从地沿相同路线出发徒步前往地进行物资捐献，甲出发1分钟后乙再出发，一段时间后乙追上甲，这时甲发现有东西落在地，于是原路原速返回地去取（甲取东西的时间忽略不计），而乙继续前行，甲乙两人到达B地后原地帮忙．已知在整个过程中，甲乙均保持各自的速度匀速行走，甲、乙两人相距的路程（米）与甲出发的时间（分钟）之间的函数关系如图所示，则当乙到达地时，甲距地的路程是_______米．

    【答案】160

    【解析】

    根据题意和函数图象中的数据可以求得甲、乙的速度，从而可以解答本题．

    由题意得，甲的速度为：80÷1=80（米/分钟），

    乙的速度为：（80×5-16）÷（5-1）=96（米/分钟），

    甲乙到达C地的时间为第t分钟，则80t=96（t-1），得t=6，

    乙从C地到B地用的时间为：（864-80×6）÷96=4（分钟），

    ∴乙到达B地时，甲与A地相距的路程是：80×（6-4）=160（米），

    故答案为：160米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

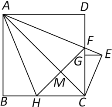
    【题目】如图，在边长为2的正方形ABCD中，AE平分∠DAC，AE交CD于点F，CE⊥AE，垂足为点E，EG⊥CD，垂足为点G，点H在边BC上，BH＝DF，连接AH、FH，FH与AC交于点M．下面结论：①FH＝2BH；②AC⊥FH；③DF＝1；④ EG2＝FGDG．其中正确的个数为（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

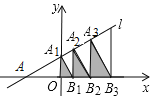
    【题目】如图，直线l：y=分别交x轴、y轴于点A和点A1，过点A1作A1B1⊥l，交x轴于点B1，过点B1作B1A2⊥x轴，交直线l于点A2；过点A2作A2B2⊥l，交x轴于点B2，过点B2作B2A3⊥x轴，交直线l于点A3；依此规律...若图中阴影△A1OB1的面积为S1，阴影△A2B1B2的面积S2，阴影△A3B2B3的面积S3...，则Sn=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与轴交于，两点，与轴交于点，点是抛物线的顶点．

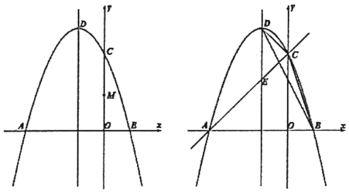
    （1）求抛物线的解析式；

    （2）点是轴正半轴上的一点，，点在对称轴左侧的抛物线上运动，直线交抛物线的对称轴于点，连接，当平分时，求点的坐标；

    （3）直线交对称轴于点，是坐标平面内一点，当与全等时，请直接写出点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】植树节来临之际，学校准备购进一批树苗，已知2棵甲种树苗和5棵乙种树苗共需113元；3棵甲种树苗和2棵乙种树苗共需87元．

    （1）求一棵甲种树苗和一棵乙种树苗的售价各是多少元？

    （2）学校准备购进这两种树苗共100棵，并且乙种树苗的数量不多于甲种树苗数量的2倍，请设计出最省钱的购买方案，并求出此时的总费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在初中阶段的函数学习中，我们经历了“确定函数的表达式——利用函数图象研究其性质——应用函数解决问题”的学习过程．在画函数图象时，我们可以通过描点或平移的方法画出一个函数的大致图象，结合上面经历的学习过程，现在来解决下面问题：

    在函数中，当时，；当时，．

    （1）求这个函数的表达式；

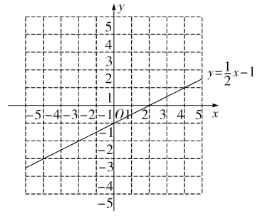
    （2）在给出的平面直角坐标系中，请用你喜欢的方法画出这个函数的图象，并写出这个函数的一条性质；

    （3）已知函数的图象如图所示，结合你所画的函数图象，直接写出不等式的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P．

    （1）求证：PD是⊙O的切线；

    （2）求证：△ABD∽△DCP；

    （3）当AB=5cm，AC=12cm时，求线段PC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】水产公司有一种海产品共2104千克，为寻求合适的销售价格，进行了8天试销，试销情况如下：

    第1天

    第2天

    第3天

    第4天

    第5天

    第6天

    第7天

    第8天

    售价(元/千克)

    400

    300

    250

    240

    200

    150

    125

    120

    销售量(千克)

    30

    40

    48

    50

    60

    80

    96

    100

    观察表中数据，发现可以用反比例函数刻画这种海产品每天的销售量(千克)与销售价格(元/千克)之间的关系．现假定在这批海产品的销售中，每天的销售量(千克)与销售价格(元/千克)之间都满足这一关系．

    （1）写出这个反比例函数的解析式；

    （2）在试销8天后，公司决定将这种海产品的销售价格定为150元/千克，并且每天都按这个价格销售，那么余下的这些海产品预计再用多少天可以全部售出？

    （3）在按（2）中定价继续销售15天后，公司发现剩余的这些海产品必须在不超过2天内全部售出，此时需要重新确定一个销售价格，使后面两天都按新的价格销售，那么新确定的价格最高不超过每千克多少元才能完成销售任务？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB经过⊙O上的点C，并且OA＝OB，CA＝CB，⊙O交直线OB于E，D，连接EC，CD．

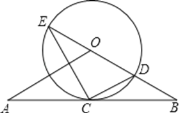
    （1）求证：直线AB是⊙O的切线；

    （2）试猜想BC，BD，BE三者之间的等量关系，并加以证明；

    （3）若tan∠CED＝，⊙O的半径为3，求OA的长．

    查看答案和解析>>

    同步练习册答案