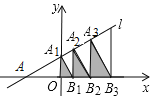
【题目】如图，直线l：y=分别交x轴、y轴于点A和点A1，过点A1作A1B1⊥l，交x轴于点B1，过点B1作B1A2⊥x轴，交直线l于点A2；过点A2作A2B2⊥l，交x轴于点B2，过点B2作B2A3⊥x轴，交直线l于点A3；依此规律...若图中阴影△A1OB1的面积为S1，阴影△A2B1B2的面积S2，阴影△A3B2B3的面积S3...，则Sn=__________．

【答案】

【解析】

由直线l：y=可求出与x轴交点A的坐标，与y轴交点A1的坐标，进而得到OA，OA1的长，也可求出Rt△OAA1的各个内角的度数，是一个特殊的直角三角形，以下所作的三角形都是含有30°角的直角三角形，然后这个求出S1、S2、S3、S4、……根据规律得出Sn．

对于直线l：y=，当x=0时，y=1；当y=0时，x=-

∴A（-，0）A1（0，1）

∴∠OAA1=30°

又∵A1B1⊥l，

∴∠OA1B1=30°，

在Rt△OA1B1中，，

∴；

同理可求出：，

∴；

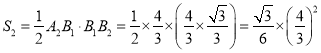依次可求出：……

因此：=

故答案为：．

关闭