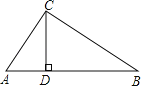
【题目】如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.
求:
(1)△ABC的面积;
(2)CD的长;
(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(4)作出△BCD的边BC边上的高DF,当BD=11cm时,试求出DF的长.
参考答案:
【答案】(1)S△ABC=30cm2,(2)CD=![]() cm,(3)S△ABE=15cm2,(4)DF=
cm,(3)S△ABE=15cm2,(4)DF=![]() cm.
cm.
【解析】
试题分析:(1)根据直角三角形面积的求法,即可得出△ABC的面积,
(2)根据三角形的面积公式即可求得CD的长,
(3)根据中线的性质可得出△ABE和△BCE的面积相等,从而得出答案,
(4)过D点作DF垂直于BC交BC与F,根据△BCD的面积即可求出DF.
解:(1)∵∠ACB=90°,BC=12cm,AC=5cm,
∴S△ABC=![]() BC×AC=30cm2,
BC×AC=30cm2,
(2)∵S△ABC=![]() AB×CD=30cm2,
AB×CD=30cm2,
∴CD=30÷![]() AB=
AB=![]() cm,
cm,
(3)S△ABE=![]() S△ABC=
S△ABC=![]() ×30=15cm2,
×30=15cm2,
(4)∵S△BCD=![]() BD×CD=
BD×CD=![]() BCDF,
BCDF,
∴BDCD=BCDF,
∴11×![]() =12×DF,
=12×DF,
∴DF=11×![]() =
=![]() cm.
cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市举行的中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
人数
1
2
4
3
3
2
这些运动员跳高成绩的中位数和众数分别是( )
A. 1.70,1.65 B. 1.70,1.70 C. 1.65,1.70 D. 3,4
-
科目: 来源: 题型:
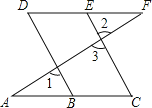
查看答案和解析>>【题目】如图,已知∠1=∠2,∠C=∠D,请问∠A与∠F相等吗?请说明理由.
解:∠A=∠F
∵ ∠1=∠2
又 ∵∠3=∠2 ( )∴∠1=∠3 ( )
∴BD∥CE ( )
∴∠ABD=∠C ( )
又∵∠C=∠D ∴∠ABD=∠D
∴
∴∠A=∠F ( )
-
科目: 来源: 题型:
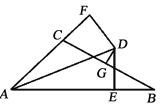
查看答案和解析>>【题目】如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=11,AC=5,则BE=______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,四边形ABCD四个顶点的坐标分别为A(-2,0),B(-1,2),C(3,3),D(4, 0).
(1)画出四边形ABCD;
(2)把四边形ABCD向下平移4个单位长度,再向左平移2个单位长度得到四边形A′B′C′D′,画出四边形A′B′C′D′,并写出C′的坐标。
(3)求出四边形ABCD的面积。

-
科目: 来源: 题型:
查看答案和解析>>【题目】若2m=4,4n=8,则2m+2n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣2x+3的对称轴是直线( )
A. x=﹣2 B. x=2 C. x=﹣1 D. x=1
相关试题

