【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC,BE=BC.当∠CBE:∠BCE=_________,求证:四边形ABCD是正方形.

参考答案:
【答案】2:3,证明见解析.
【解析】
首先证得△ADE≌△CDE,由全等三角形的性质可得∠ADE=∠CDE,由AD∥BC可得∠ADE=∠CBD,可得∠CDB=∠CBD,可得BC=CD,可得AD=BC,利用平行四边形的判定定理可得四边形ABCD为平行四边形,由AD=CD可得四边形ABCD是菱形; 由BE=BC可得△BEC为等腰三角形,可得∠BCE=∠BEC,利用三角形的内角和定理可得∠CBE =45°,可得∠ABE=45°,可得∠ABC=90°,由正方形的判定定理可得四边形ABCD是正方形.
证明:当∠CBE:∠BCE=![]() 时,四边形ABCD是正方形.
时,四边形ABCD是正方形.
理由如下:
在△ADE与△CDE中,
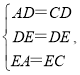
∴∠ADE=∠CDE,
∵AD∥BC,
∴∠ADE=∠CBD,
∴∠CDE=∠CBD,
∴BC=CD,
∵AD=CD,
∴BC=AD,
∴四边形ABCD为平行四边形,
∵AD=CD,
∴四边形ABCD是菱形;
∵BE=BC
∴∠BCE=∠BEC,
∵∠CBE:∠BCE=2:3,
∴∠CBE=180×![]() =45°,
=45°,
∵四边形ABCD是菱形,
∴∠ABE=45°,
∴∠ABC=90°,
∴四边形ABCD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,
 .求BE的长.
.求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
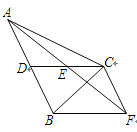
(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,
 D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使 ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF
(1)求证:四边形EDFG是正方形;
(2)直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在一块宽为12m,长为20m的矩形地面上修筑同样宽的道路,余下的部分种上草坪.要使草坪的面积为180m2,求道路的宽;
(2)现在对该矩形区域进行改造,如图2,在正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行的且宽度相等的道路,已知道路的宽为正方形边长的
 .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的 ,求道路的宽.
,求道路的宽.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.

(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中每个小方格的边长为1,且点A,B,C均为格点.

(1)画出△ABC关于直线l的对称图形△A1B1C1;
(2)求△ABC的面积;
(3)边AB=_____________(不用写过程);
(4)在直线l上找一点D,使AD+BD最小.
相关试题

