【题目】如图1,已知l1∥l2 , 点A,B在直线l1上,点C,D在l2上,连接AD,BC.AE,CE分别是∠BAD,∠BCD的平分线,∠1=70°,∠2=30°. 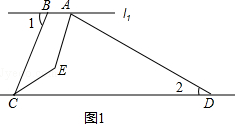
(1)求∠AEC的度数;
(2)如图2,将线段AD沿线段CD方向平移,其他条件不变,求∠AEC的度数. 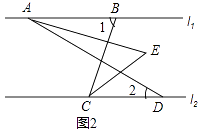
参考答案:
【答案】
(1)解:如图1,过点E作EF∥l1,

∵l1∥l2,
∴EF∥l2,
∵l1∥l2,
∴∠BCD=∠α,
∵∠1=70°,
∴∠BCD=70°,
∵CE是∠BCD的角平分线,
∴∠ECD= ![]() ×70°=35°,
×70°=35°,
∵EF∥l2,
∴∠FEC=∠ECD=35°,
∵l1∥l2,
∴∠BAD+∠2=180°,
∵∠2=30°,
∴∠BAD=150°,
∵AE平分∠BAD,
∴∠BAE= ![]() ×150°=75°,
×150°=75°,
∵EF∥l1,
∴∠BAE+∠AEF=180°,
∴∠AEF=105°,
∴∠AEC=105°+35°=140°
(2)解:如图2,过点E作EF∥l1,

∵l1∥l2,
∴EF∥l2,
∵l1∥l2,
∴∠BCD=∠1,
∵∠1=70°,
∴∠BCD=70°,
∵CE是∠BCD的角平分线,
∴∠ECD= ![]() ×70°=35°,
×70°=35°,
∵EF∥l2,
∴∠FEC=∠ECD=35°,
同理可求∠AEF=15°,
∴∠AEC=∠AEF+∠CEF=50°
【解析】(1)利用平行线的性质结合角平分线的性质得出∠BAE以及∠AEF的度数即可得出答案;(2)利用平行线的性质结合角平分线的性质得出∠ECD以及∠AEF的度数即可得出答案.
【考点精析】本题主要考查了平行线的性质和平移的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从国家旅游局获悉,2017年春节期间,全国共接待游客3.44亿人次,实现旅游总收入423300000000元.将423300000000元用科学记数法表示为( )
A.4.233×103元
B.0.4233×104元
C.42.33×1010元
D.4.233×1011元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线

(1)填空:抛物线的顶点坐标是( , ),对称轴是 ;
(2)已知y轴上一点A(0,-2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点 N,使以点O、点A、点M、点N为顶点的四边形为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x+3的图象向左平移一个单位,再向上平移两个单位后,所得二次函数的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】大众创业,万众创新,据不完全统计,2015年毕业的大学生中创业人数已经达到7490000人,将7490000这个数据用科学记数法表示为( )
A.7.49×107
B.7.49×106
C.74.9×106
D.0.749×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)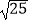 ﹣
﹣ 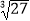 +
+ 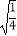 ;
;
(2)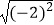 +|
+| 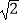 ﹣1|﹣(
﹣1|﹣( 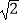 +1).
+1).
(3)(﹣ )2+
)2+  ﹣(2﹣
﹣(2﹣ 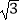 )+|2﹣
)+|2﹣ 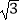 |
|
相关试题

