【题目】已知,AB∥CD,AB,CD被直线l所截,点P是l上的一动点,连接PA,PC.
(1)如图①,当P在AB,CD之间时,求证:∠APC=∠A+∠C; 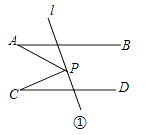
(2)如图②,当P在射线ME上时,探究∠A,∠C,∠APC的关系并证明; 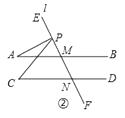
(3)如图③,当P在射线NF上时,直接写出∠A,∠C,∠APC三者之间关系. 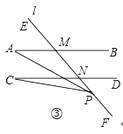
参考答案:
【答案】
(1)证明:如图①,过P点作,PE∥AB,则:∠A=∠APE,
∵AB∥CD,
∴PE∥CD
∴∠EPC=∠C.
又∵∠APC=∠APE+∠EPC,
∴∠APC=∠A+∠C
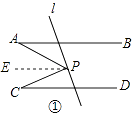
(2)解:如图②,
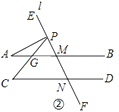
∵AB∥CD,
∴∠C=∠PGM.
∵∠PGM=∠A+∠APC,
∴∠C=∠A+∠APC
(3)解:如图③,
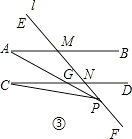
∵AB∥CD,
∴∠A=∠AGC.
∵∠AGC=∠C+∠APC,
∴∠A=∠C+∠APC.
【解析】(1)过P点作PE∥AB,则∠A=∠APE,再由AB∥CD得出PE∥CD,故∠EPC=∠C,利用等量代换即可得出结论;(2)先由平行线的性质得出∠C=∠PGM,再由三角形外角的性质即可得出结论;(3)根据AB∥CD得出∠A=∠AGC,再由三角形外角的性质即可得出结论.
【考点精析】通过灵活运用平行线的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于a,b的多项式(a2+2ab﹣b2)﹣(a2+mab+2b2)中不含ab项,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年3月5日召开十三届全国人大二次会议,政府工作报告中提到2012年我国的贫困人口为9899万人,2018年减少到1660万人,连续6年平均每年减贫1300多万人,将数据1300万用科学记数法可表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个(记为A1,A2,A3),黑球2个(记为B1,B2).
(1)若先从袋中取出m(m>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:①若A为必然事件,则m的值为 ②若A为随机事件,则m的取值为
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用树状图或列表法求这个事件的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=﹣
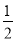 x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.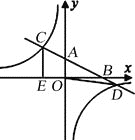
(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
-
科目: 来源: 题型:
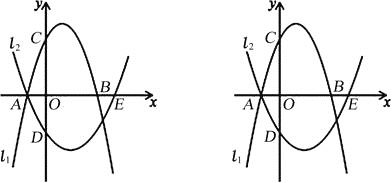
查看答案和解析>>【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).
(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.
相关试题

