【题目】已知关于x的方程kx2+4x-2=0有实数根,求k的取值范围.
参考答案:
【答案】K的取值范围为k≥-2.
【解析】试题分析:根据题意,分两种情况可知:
当k=0时,直接判断一元一次方程的解的可能即可;
当k≠0时,根据一元二次方程根的判别式判断根的情况即可.
试题解析:当k=0时,方程变为一元一次方程4x-2=0,此时方程有实数根,
当K≠0时,
∵关于x的方程kx2+4x-2=0有实数根,
∴△=b2-4ac≥0,
即:16+8k≥0,
解得:k≥-2,
∴K的取值范围为k≥-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,与(﹣a+1)2相等的是( )
A.a2﹣1
B.a2+1
C.a2﹣2a+1
D.a2+2a+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程ax2+bx+5=0(a≠0)的一个解是x=1,则2 017-a-b的值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为△ABC三边,且满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果收入15元记作+15元,那么支出20元记作( )元.
A.+5
B.+20
C.﹣5
D.﹣20 -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究:如图,抛物线y=﹣
 x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,过点B作线段BC⊥x轴,交直线y=﹣2x于点C.
x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,过点B作线段BC⊥x轴,交直线y=﹣2x于点C.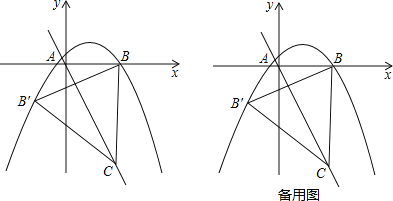
(1)求该抛物线的解析式;
(2)求点B关于直线y=﹣2x的对称点B′的坐标,判定点B′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段B′C于点D,是否存在这样的点P,使四边形PBCD是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的计算正确的是( )
A.6a-5a=1
B.a+2a2=2a3
C.-(a-b)= -a+b
D.2(a+b) =2a+b
相关试题

