Question

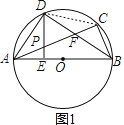
【题目】已知：如图，△ABC内接于⊙O，AB为直径，点D是弧AC上的一点，连接AD、BD，AC交BD于点F，DE⊥AB于点E，交AC于点P，∠ABD=∠CBD=∠CAD．

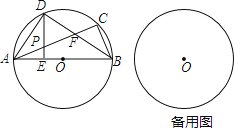
（1）求证：PA=PD；

（2）判断AP与PF是否相等，并说明理由；

（3）当点C为半圆弧的中点，小李通过操作发现BF=2AD，请问小李的发现是否正确？若正确，请说明理由；若不正确，请写出BF与AD正确的关系式．

Answer 1

【答案】（1）见解析；（2）相等，理由见解析；（3）小李的发现是正确的，理由见解析

【解析】

试题分析：（1）如图1，连接CD，由AB是半⊙O的直径，DE⊥AB于E，得到∠DBA+∠DAB=∠ADE+∠DAE=90°，于是得到∠DBA=∠ADE，根据圆周角定理得到∠DCA=∠DBA=∠DAC，即可求出结论；

（2）根据圆周角定理求出∠DAP=∠ADP，求出AP=DP，求出∠BDE=∠DAE，求出DP=FP，即可得出答案；

（3）根据全等三角形的性质和判定求出AD=BF，DA=DG，即可得出答案．

解：（1）如图1，连接CD，

∵AB是半⊙O的直径，

∴∠ADB=90°，

∵DE⊥AB于E，

∴∠DEA=90°，

∴∠DBA+∠DAB=∠ADE+∠DAE=90°，

∴∠DBA=∠ADE，

∵点D是弧AC的中点，

∴∠DCA=∠DBA=∠DAC，

∴∠DAP=∠ADP，

∴AP=DP；

（2）AP=PF；

理由是：∵AB是直径，DE⊥AB，

∴∠ADB=∠DEB=90°，

∴∠ADE=∠ABD，

∵D为弧AC中点，

∴∠DAC=∠DBA，

∴∠ADE=∠DAC，

∴AP=DP，∠FDE=∠AFD，

∴DP=PF，

∴AP=PF；

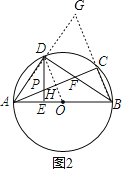
（3）小李的发现是正确的，

理由是：如图2，延长AD、BC，两线交于G，

∵C为半圆弧的中点，D是弧AC的中点，

∴∠CBD=∠GAC，∠BCA=∠ACG=90°，AC=BC，

在△CBF和△CAG中，

，

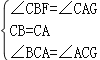∴△CBF≌△CAG（ASA），

∴BF=AG，

∵BC为直径

∴∠ADB=90°，

∵D为弧AC中点，

∴∠GBD=∠ABD

在△ADB和△GDB中，

，

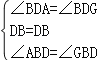∴△ADB≌△GDB（ASA），

∴DG=DA=AG，

∴BF=2AD．