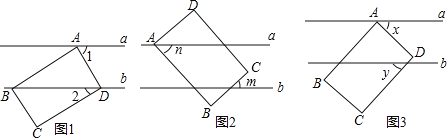
【题目】如图,已知a∥b,长方形ABCD的点A在直线a上,B,C,D三点在平面上移动变化(长方形形状大小始终保持不变),请根据如下条件解答:
(1)图1,若点B、D在直线b上,点C在直线b的下方,∠2=30°,则∠1= ;
(2)图2,若点D在直线a的上方,点C在平行直线a,b内,点B在直线b的下方,m,n表示角的度数,请写出m与n的数量关系并说明理由;
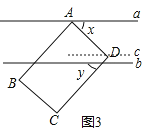
(3)图3,若点D在平行直线a,b内,点B,C在直线b的下方,x,y表示角的度数(x>y),且满足关系式x2﹣2xy+y2=100,求x的度数.
参考答案:
【答案】(1)60°;(2)90°;(3)50°
【解析】(1)首先根据角的和差关系计算出∠ADB的度数,再根据平行线的性质可得∠1的度数;(2)过C作EF∥a,根据a∥b可得EF∥a∥b, 再根据平行线的性质可得∠4+m=∠BCD,n=∠4,利用等量代换可得答案;(3)过D作c∥b,根据条件可得x-y=10,再根据平行线的性质可得x+y=90,两个方程组合可得答案.
解:(1)∵四边形ABCD是长方形,
∴∠ADC=90°,
∵∠2=30°,
∴∠ADB=60°,
∵a∥b,
∴∠1=∠ADB=60°,
故答案为:60°;
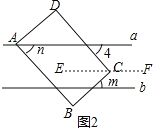
(2)如图2,过C作EF∥a,
∵AB∥CD,
∴n=∠4,
∵a∥b,
∴EF∥a∥b,
∴∠4+m=∠BCD=90°,
∴m+n=90°;
(3)如图3,过D作c∥b,
∵a∥b,
∴a∥b∥c,
∵x2﹣2xy+y2=100,
∴(x﹣y)2=100,
∵x>y,
∴x﹣y=﹣10(舍去),
∴x﹣y=10,①
∵a∥b,
∴a∥b∥c,
∵∠ADC=90°,
∴x+y=90,②
①+②得:x=50°.
“点睛”此题考查了四边形综合,以及平行线的性质和判定,关键是掌握两直线平行,内错角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明:在△ABC中,如果M、N分别是边AB、AC上的点,那么BN、CM不能互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校计算机考试情况,抽取了50名学生的计算机考试成绩进行统计,统计结果如表所示,则50名学生计算机考试成绩的众数、中位数分别为( )
考试分数(分)
20
16
12
8
人数
24
18
5
3
A. 20,16B. l6,20C. 20,l2D. 16,l2
-
科目: 来源: 题型:
查看答案和解析>>【题目】点M(-6,5)到x轴的距离是_____,到y轴的距离是______.
-
科目: 来源: 题型:
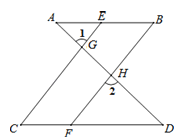
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD(___ ___)
∴∠2=∠CGD(等量代换)
∴CE∥BF(__ ___)
∴∠____ ____=∠BFD(___ ____)
又∵∠B=∠C(已知)
∴____ ____(等量代换)
∴AB∥CD(___ ____)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆轿车从甲地出发开往乙地,同时,一辆客车从乙地开往甲地,一开始两车的速度相同,出发半小时后,客车因出现故障维修了一段时间,修好后为了不耽误乘客的时间,客车加快速度前进,结果与轿车同时到达各自的目的地.设轿车出发th后,与客车的距离为Skm,图中的折线(A→B→C→D→E)表示S与t之间的函数关系.
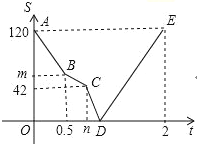
(1)甲、乙两地相距 km,轿车的速度为 km/h;
(2)求m与n的值;
(3)求客车修好后行驶的速度;
(4)求线段DE所对应的函数关系式,并注明自变量的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元.2016年投入教育经费8640万元.假设该县这两年投入教育经费的年平均增长率相同.
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元.
相关试题

