[题目]从下列算式:①,②26÷23＝4,③ -12018＝1,④ (-)2＝3,⑤a+a＝a2中随机抽取一个.运算结果正确的概率是( )A. B. C. D. 题目和参考答案 ——青夏教育精英家教网—

【题目】从下列算式：①；②26÷23＝4；③ －12018＝1；④ （－）2＝3；⑤a＋a＝a2中随机抽取一个，运算结果正确的概率是（）

A. B. C. D.

参考答案：

【答案】A

【解析】

根据二次根式、整数指数幂以及随机事件的概率的定义进行求解即可.

①由算术平方根的概念得, =3,故①项错误;

②由“同底数幂相除, 底数不变, 指数相减”得, 26÷23=26-3=23=8,故②项错误;

③由整数指数幂的性质得: －12018=-1, 故③项错误;

④由整数指数幂的性质得, （－）2＝3,故④项正确;

⑤合并同类项得, a+a=2a,故⑤项错误,

综上所述,5个运算结果中正确的共有1个,

故运算结果正确的概率P=,

故本题正确答案为A.

相关试题

科目： 来源： 题型：

【题目】已知a+b＝1，ab＝﹣1，设S1＝a+b，S2＝a2+b2，S3＝a3+b3，…，Sn＝an+bn
（1）计算S2．
（2）请阅读下面计算S3的过程：
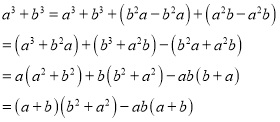
∵a+b＝1，ab＝﹣1
∴S3＝a3+b3＝（a+b）（a2+b2）﹣ab（a+b）＝1×S2﹣（﹣1）＝S2+1＝　　．
你读懂了吗？请你先填空完成（2）中S3的计算结果，再用你学到的方法计算S4
（3）试写出Sn﹣2，Sn﹣1，Sn三者之间的数量关系式（不要求证明，且n是不小于2的自然数），根据得出的数量关系计算S7．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，AB是⊙O的直径，点C、D在⊙O上，∠A=2∠BCD，点E在AB的延长线上，∠AED=∠ABC
（1）求证：DE与⊙O相切；
（2）若BF=2，DF=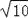，求⊙O的半径．
查看答案和解析>>
科目： 来源： 题型：

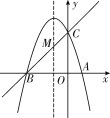
【题目】如图，已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝－1，且经过A(1,0)，C(0，3)两点，与x轴的另一个交点为B.
(1)若直线y＝mx＋n经过B，C两点，求直线BC和抛物线的解析式；
(2)在抛物线的对称轴x＝－1 上找一点M，使点M到点A的距离与到点C的距离之和最小，求点M的坐标．
查看答案和解析>>
科目： 来源： 题型：

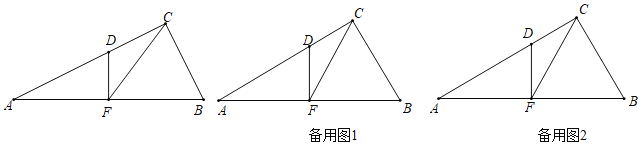
【题目】如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AB＝12，点F是AB的中点，过点F作FD⊥AB交AC于点D．
（1）若△AFD以每秒2个单位长度的速度沿射线FB向右移动，得到△A1F1D1，当F1与点B重合时停止移动．设移动时间为t秒，△A1F1D1与△CBF重叠部分的面积记为S．直接写出S与t的函数关系式．
（2）在（1）的基础上，如果D1，B，F构成的△D1BF为等腰三角形，求出t值．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，抛物线y＝ax2＋bx＋c（a≠0）的对称轴为直线x＝1，且经过点（﹣1，0），下列四个结论：①如果点（，y1）和（2，y2）都在抛物线上，那么y1＜y2；②b2﹣4ac＞0；③m（am＋b）＜a＋b（m≠1的实数）；④；其中正确的有（　　）
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目： 来源： 题型：

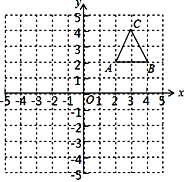
【题目】如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，2）请解答下列问题：
（1）画出△ABC关于原点O成中心对称的△A1B1C1，并写出A1的坐标；
（2）画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2，并求出点C在旋转过程中经过的路径长是多少？
查看答案和解析>>