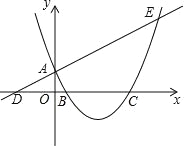
【题目】如图,已知直线y=![]() x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y=![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
(1)求该抛物线的解析式;
(2)在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标;
(3)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标.
参考答案:
【答案】(1)y=x2﹣x+1;(2)M(![]() ,﹣
,﹣![]() ).(3)点P的坐标为(,0)或(1,0)或(3,0)或(
).(3)点P的坐标为(,0)或(1,0)或(3,0)或(![]() ,0).
,0).
【解析】
试题分析:(1)根据直线的解析式求得点A(0,1),那么把A,B坐标代入y=![]() x2+bx+c即可求得函数解析式.
x2+bx+c即可求得函数解析式.
(2)易得|AM﹣MC|的值最大,应找到C关于对称轴的对称点B,连接AB交对称轴的一点就是M.应让过AB的直线解析式和对称轴的解析式联立即可求得点M坐标.
(3)让直线解析式与抛物线的解析式结合即可求得点E的坐标.△PAE是直角三角形,应分点P为直角顶点,点A是直角顶点,点E是直角顶点三种情况探讨.
试题解析:(1)将A(0,1)、B(1,0)坐标代入y=x2+bx+c
得 ,
,
解得: .
.
∴物线的解折式为y=x2﹣x+1;
(2)抛物线的对称轴为x=![]() ,B、C关于x=
,B、C关于x=![]() 对称,
对称,
∴MC=MB,
要使|AM﹣MC|最大,即是使|AM﹣MB|最大,
由三角形两边之差小于第三边得,当A、B、M在同一直线上时|AM﹣MB|的值最大.
知直线AB的解析式为y=﹣x+1
∴ ,
,
解得: .
.
则M(![]() ,﹣
,﹣![]() ).
).
(3)设点E的横坐标为m,则它的纵坐标为m2﹣m+1,
即E点的坐标(m,m2﹣m+1),…
又∵点E在直线y=x+1上,
∴m2﹣m+1=m+1
解得m1=0(舍去),m2=4,
∴E的坐标为(4,3).
(Ⅰ)当A为直角顶点时,
过A作AP1⊥DE交x轴于P1点,设P1(a,0)易知D点坐标为(﹣2,0),
由Rt△AOD∽Rt△P1OA得
![]() ,即
,即![]() ,
,
∴a=![]() ,a=-
,a=-![]() (舍去),
(舍去),
∴P1(![]() ,0).
,0).
(Ⅱ)同理,当E为直角顶点时,过E作EP2⊥DE交x轴于P2点,
由Rt△AOD∽Rt△P2ED得,
![]() 即:
即:![]() ,
,
∴EP2=![]()
∴DP2=![]()
∴a=![]() ,
,
∴P2点坐标为(![]() ,0).
,0).
(Ⅲ)当P为直角顶点时,过E作EF⊥x轴于F,设P3(b、0),
由∠OPA+∠FPE=90°,得∠OPA=∠FEP,Rt△AOP∽Rt△PFE,
由![]() 得:
得:![]() ,
,
解得b1=3,b2=1,
∴此时的点P3的坐标为(1,0)或(3,0),
综上所述,满足条件的点P的坐标为(,0)或(1,0)或(3,0)或(![]() ,0).
,0).

-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式x2-6x-b可化为(x+a)2-1,则b的值是 ______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋中,红色、黑色、白色的玻璃球共有50个,除颜色外,形状、大小、质地完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率分别稳定在20%和40%,则布袋中白色球的个数很可能是个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分7分)完成下列各题:
(1)如图,在矩形
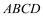 中,AF=BE. 求证:DE=CF;
中,AF=BE. 求证:DE=CF;(2)如图,
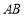 是
是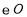 的直径,
的直径,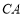 与
与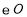 相切于点A. 连接
相切于点A. 连接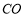 交
交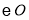 于点
于点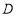 ,
,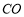 的延长线交
的延长线交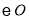 于点
于点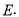 连接
连接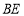 ,
,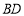 ,
,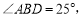 求
求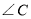 的度数.
的度数.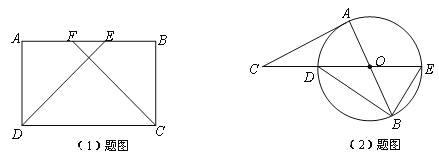
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的盒子中放有四张分别写有数字1,2,3,4的红色卡片和三张分别写有数字1,2,3的蓝色卡片,卡片除颜色和数字外完全相同.
(1)从中任意抽取一张卡片,求该卡片上写有数字1的概率;
(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋中,红色、黑色、白色的玻璃球共有20个,除颜色外其他完全相同.小明通过多次摸球试验后发现其中摸到红色、黑色球的频率分别稳定在15%和45%,则口袋中白色球很可能有个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在硬地上掷1枚图钉,通常会出现两种情况:“钉尖着地”与“钉尖不着地”.任意重复抛掷1枚图钉很多次时,你认为是哪种情况的可能性大( )
A.钉尖着地
B.钉尖不着地
C.一样大
D.不能确定
相关试题

