【题目】已知直线l上有一点O,点A、B同时从O出发,在直线l上分别向左、向右作匀速运动,且A、B的速度比为1:2,设运动时间为ts.

(1)当t=2s时,AB=12cm.此时,
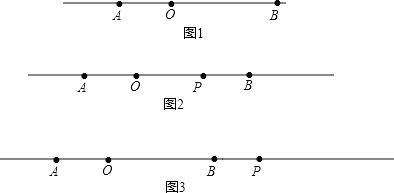
①在直线l上画出A、B两点运动2秒时的位置,并回答点A运动的速度是 cm/s; 点B运动的速度是 cm/s.
②若点P为直线l上一点,且PA﹣PB=OP,求![]() 的值;
的值;
(2)在(1)的条件下,若A、B同时按原速向左运动,再经过几秒,OA=2OB.
参考答案:
【答案】(1)①2,4;②![]() 或1(2)
或1(2)![]() 或
或![]()
【解析】
试题分析:(1)①设A的速度为xcm/s,B的速度为2xcm/s,根据2s相距的距离为12建立方程求出其解即可;
②分情况讨论如图2,如图3,建立方程求出OP的值就可以求出结论;
(2)设A、B同时按原速向左运动,再经过几a秒OA=2OB,根据追击问题的数量关系建立方程求出其解即可.
解:(1)①设A的速度为xcm/s,B的速度为2xcm/s,由题意,得
2x+4x=12,
解得:x=2,
∴B的速度为4cm/s;
故答案为:2,4
②如图2,当P在AB之间时,
∵PA﹣OA=OP,PA﹣PB=OP,
∴PA﹣OA=PA﹣PB,
∴OA=PB=4,
∴OP=4.
∴![]() .
.
如图3,当P在AB的右侧时,
∵PA﹣OA=OP,PA﹣PB=OP,
∴PA﹣OA=PA﹣PB,
∴OA=PB=4,
∴OP=12.
∴![]()
答:![]() =
=![]() 或1;
或1;
(2)设A、B同时按原速向左运动,再经过几a秒OA=2OB,由题意,得
2a+4=2(8﹣4a)或2a+4=2(4a﹣8)
解得:a=![]() 或
或![]()
答:再经过![]() 或
或![]() 秒时OA=2OB.
秒时OA=2OB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程x2 +2x-3 = 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,D为AB上任一点,过D作AB的垂线,分别交边AC、BC的延长线于E、F两点,∠BAC、∠BFD的平分线交于点I,AI交DF于点M,FI交AC于点N,连接BI.下列结论:①∠BAC=∠BFD;②∠ENI=∠EMI;③AI⊥FI;④∠ABI=∠FBI;其中正确结论的个数是( )
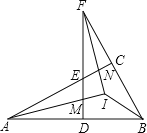
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s,点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s,连接PQ,若设运动的时间为t(s)(0<t<2),解答下列问题:
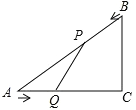
(1)设△AQP的面积为y(cm2),求y与t之间的函数关系式;
(2)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论:①BD平分∠ABC;②AD=BD=BC;③△BDC的周长等于AB+BC;④D是AC中点.其中正确的命题序号是( )

A.①②③ B.①②④ C.②③④ D.①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去 B.带②去 C.带③去 D.带①和②去
相关试题

