【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB=![]() CD,求⊙O半径.
CD,求⊙O半径.

参考答案:
【答案】(1)见解析;(2)![]()
【解析】分析: (1)首先连接CO,根据CD与⊙O相切于点C,可得:∠OCD=90°;然后根据AB是圆O的直径,可得:∠ACB=90°,据此判断出∠CAD=∠BCD,即可推得△ADC∽△CDB.
(2)首先设CD为x,则AB=32x,OC=OB=34x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得:ACCB=CDBD,据此求出CB的值是多少,即可求出⊙O半径是多少.
详解:
(1)证明:如图,连接CO,
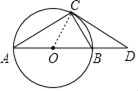 ,
,
∵CD与⊙O相切于点C,
∴∠OCD=90°,
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠ACO=∠BCD,
∵∠ACO=∠CAD,
∴∠CAD=∠BCD,
在△ADC和△CDB中,
![]()
∴△ADC∽△CDB.
(2)解:设CD为x,
则AB=![]() x,OC=OB=
x,OC=OB=![]() x,
x,
∵∠OCD=90°,
∴OD=![]() =
=![]() =
=![]() x,
x,
∴BD=OD﹣OB=![]() x﹣
x﹣![]() x=
x=![]() x,
x,
由(1)知,△ADC∽△CDB,
∴![]() =
=![]() ,
,
即![]() ,
,
解得CB=1,
∴AB=![]() =
=![]() ,
,
∴⊙O半径是![]() .
.
点睛: 此题主要考查了切线的性质和应用,以及勾股定理的应用,要熟练掌握.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明将一个正方形纸剪去一个宽为
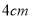 的长条后, 再从剩下的长方形纸片上剪去一个宽为
的长条后, 再从剩下的长方形纸片上剪去一个宽为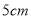 的长条,如果两次剪下的长条面积正好相等,那么剩下的白色长方形纸的面积为( )
的长条,如果两次剪下的长条面积正好相等,那么剩下的白色长方形纸的面积为( )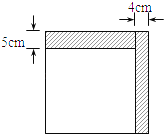
A.
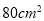 B.
B.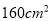 C.
C.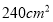 D.
D.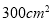
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=AC.D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①△AED≌△AEF;
②△ABE∽△ACD;
③BE+DC=DE;
④BE2+DC2=DE2.
其中正确的是( )

A.②④ B.①④ C.②③ D.①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距
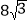 km的C处.
km的C处.(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在国家政策的宏观调控下,某市的商品房成交均价由今年3月份的14 000元/m2下降到5月份的12 600元/m2.
(1)问4,5两月平均每月降价的百分率约是多少?(参考数据:
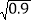 ≈0.95)
≈0.95)(2)如果房价继续跌落,按此降价的百分率,你预测到7月份该市的商品房成交均价是否会跌跛10 000元/m2?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣
 ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x2﹣2(2﹣k)x+k2+12=0有实数根α、β.
(1)求实数k的取值范围;
(2)设
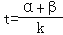 ,求t的最小值.
,求t的最小值.
相关试题

