Question

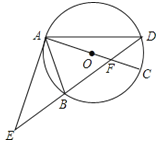
【题目】如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上一点，∠EAB=∠ADB.

（1）求证：EA是⊙O的切线；

（2）已知点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；

（3）已知AF=4，CF=2，在（2）的条件下，求AE的长.

Answer 1

【答案】(1)、证明过程见解析；(2)、证明过程见解析；(3)、AE=4

【解析】

试题分析：(1)、连接CD，根据直径所对的圆周角为直角得出∠ADB+∠EDC=90°，根据同弧所对的圆周角相等得出∠BAC=∠EDC，然后结合已知条件得出∠EAB+∠BAC=90°，从而说明切线；(2)、连接BC，根据直径的性质得出∠ABC=90°，根据B是EF的中点得出AB=EF，即∠BAC=∠AFE，则得出三角形相似；(3)、根据三角形相似得出，根据AF和CF的长度得出AC的长度，然后根据EF=2AB代入求出AB和EF的长度，最后根据Rt△AEF的勾股定理求出AE的长度.

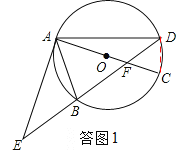
试题解析：(1)、如答图1，连接CD， ∵AC是⊙O的直径，∴∠ADC=90°. ∴∠ADB+∠EDC=90°.

∵∠BAC=∠EDC，∠EAB=∠ADB， ∴∠BAC=∠EAB+∠BAC=90°. ∴EA是⊙O的切线.

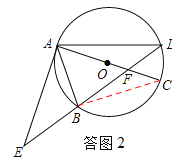
(2)、如答图2，连接BC， ∵AC是⊙O的直径，∴∠ABC=90°. ∴∠CBA=∠ABC=90°.

∵B是EF的中点，∴在Rt△EAF中，AB=BF. ∴∠BAC=∠AFE. ∴△EAF∽△CBA.

(3)、∵△EAF∽△CBA，∴. ∵AF=4，CF=2， ∴AC=6，EF=2AB.

∴，解得AB=2.∴EF=4.

∴AE=.