【题目】某校组织7年级师生外出进行研究性学习活动,学校联系了旅游公司提供车辆。该公司现有50座和35座两种车型。如果用35座的,会有5人没座位;如果全部换乘50座的,则可比35座车少用2辆,而且多出15个座位.若35座客车日租金为每辆250元,50座客车日租金为每辆300元,
(1)请你算算参加互动师生共多少人?
(2)请你设计一个方案,使租金最少,并说明理由.
参考答案:
【答案】(1)购买20盒乒乓球时,两种优惠办法付款一样;(2)购买15盒乒乓球时,去甲店较合算,购买30盒乒乓球时,去乙店较合算.
【解析】试题分析:(1)设参加互动师生共x人,那么如果用35座的需![]() 辆,全部换乘50座的需
辆,全部换乘50座的需![]() 辆,已知:如果全部换乘50座的,则可比35座车少用2辆,以此为等量关系列出方程求解;
辆,已知:如果全部换乘50座的,则可比35座车少用2辆,以此为等量关系列出方程求解;
(2)分类讨论,看什么时候所用租金最少,就选择该方案.
试题解析:
解:(1)设参加互动师生共x人,
由题意得: ![]() =
=![]() +2,
+2,
解得:x=285人,
所以,参与本次师生互动的人共有285人.
(2)设计方案为:租用1辆35座的车,租用5辆50座的车.
设租用x辆35座的,则还需租用![]() 辆50座的,其中x≥0.
辆50座的,其中x≥0.
由题意得:由于![]() =5.7≈6辆,需要租金:6×300=1800元;
=5.7≈6辆,需要租金:6×300=1800元;
所以当x=1时, ![]() =5,需要租金:250+300×5=1750元;
=5,需要租金:250+300×5=1750元;
当x=2时, ![]() =4.3≈5辆,需租金:250×2+300×5=2000元;
=4.3≈5辆,需租金:250×2+300×5=2000元;
当x=3时, ![]() =3.6≈4辆,需租金:3×250+4×300=1950元;
=3.6≈4辆,需租金:3×250+4×300=1950元;
当x=4时, ![]() =2.9≈3辆,需租金:4×250+3×300=1900元;
=2.9≈3辆,需租金:4×250+3×300=1900元;
当x=5时, ![]() =2.2≈3辆,需租金:5×250+3×300=2150元;
=2.2≈3辆,需租金:5×250+3×300=2150元;
当x=6时, ![]() =1.5≈2辆,需租金:6×250+2×300=2100元;
=1.5≈2辆,需租金:6×250+2×300=2100元;
当x=7时, ![]() =0.8≈1辆,需租金:7×250+300=2050元;
=0.8≈1辆,需租金:7×250+300=2050元;
当x=8时, ![]() ≈1辆,需租金:8×250+300=2300元;
≈1辆,需租金:8×250+300=2300元;
当x=9时,35×9>285,此时需租金:9×250=2250元;
综合上述比较当租用1辆35座的车,租用5辆50座的车时,所需资金最少.
故租35座汽车1辆,50座客车5辆最合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
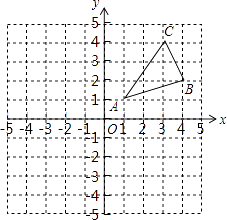
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,线段AB=5,AB∥x轴,若A点坐标为(-1,3),则B点坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知E为平行四边形ABCD中AB边上一点,且BE=AB,连接DE交BC于F,交AC于G.

(1)求证:△BEF≌△CDF;
(2)试探究OF与AB有什么位置关系和数量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y=
 x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.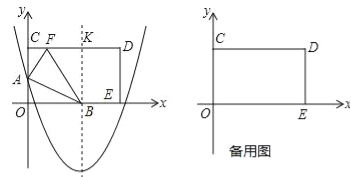
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为( 、 ),BK的长是 ,CK的长是 ;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3cm、7cm、9cm;乙盒子中装有4张卡片,卡片上分别写着2cm、4cm、6cm、8cm;盒子外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )

A. ①② B. ②③ C. ①③ D. ②④
相关试题

