【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( ) 
A.6 ![]()
B.2 ![]()
C.4 ![]()
D.4 ![]()
参考答案:
【答案】D
【解析】解:过点E作EM⊥BC于M,交BF于N, 
∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,AD=BC,
∵∠EMB=90°,
∴四边形ABME是矩形,
∴AE=BM,
由折叠的性质得:AE=GE,∠EGN=∠A=90°,
∴EG=BM,
在△ENG与△BNM中, ,
,
∴△ENG≌△BNM(AAS),
∴NG=NM,
∴CM=DE,
∵E是AD的中点,
∴AE=ED=BM=CM,
∵EM∥CD,
∴BN:NF=BM:CM,
∴BN=NF,
∴NM= ![]() CF=1,
CF=1,
∴NG=1,
∵BG=AB=CD=CF+DF=6,
∴BN=BG﹣NG=6﹣1=5,
∴BF=2BN=10,
∴BC= ![]() =
= ![]() =4
=4 ![]() .
.
故选D.
【考点精析】关于本题考查的矩形的性质和翻折变换(折叠问题),需要了解矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎.该打车方式的计价规则如图①所示,若车辆以平均速度vkm/h行驶了skm,则打车费用为(ps+60q·
 )元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.
)元(不足9元按9元计价).小明某天用该打车方式出行,按上述计价规则,其打车费用y(元)与行驶里程x(km)的函数关系也可由如图②表示.(1)当x≥6时,求y与x的函数关系式.
(2)若p=1,q=0.5,求该车行驶的平均速度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则
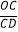 的值为( )
的值为( ) 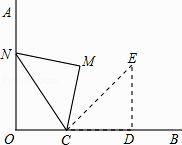
A.
B.
C.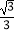
D.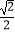
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)
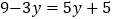
(2)
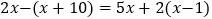
(3)
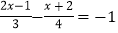
(4)
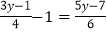
(5)
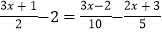
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市团委举行以“我的中国梦”为主题的知识竞赛,甲、乙两所学校的参赛人数相等,比赛结束后,发现学生成绩分别为
 分,
分,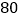 分,
分,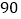 分,
分,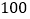 分,并根据统计数据绘制了如下不完整的统计图表:
分,并根据统计数据绘制了如下不完整的统计图表: 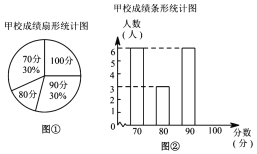
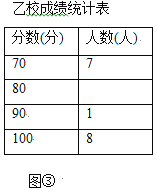
(1)乙学校的参赛人数是 人;
(2)在图①中,“
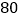 分”所在扇形的圆心角度数为 ;
分”所在扇形的圆心角度数为 ;(3)请你将图②补充完整;
(4)求乙校成绩的平均分;
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲列车速度是60km/h,乙列车速度是90km/h.
(1)两列车都从某地出发,目的地距离出发点1000km,甲列车先走2小时,问乙列车什么时候能追上甲列车?追上时离目的地还有多远?
(2)甲列车从A地开往B地,乙列车同时从B地开往A地,已知A,B两地相距200km,两车相遇的地方离A地多远?(用方程)
相关试题

