【题目】如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.
(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中, ![]() 为常数,试确定k的值.
为常数,试确定k的值.
参考答案:
【答案】
(1)
解:∵二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1,
则有  解得
解得 ![]()
∴二次函数y=x2﹣2x
(2)
解:由(1)得,B(1,﹣1),
∵A(﹣1,3),
∴直线AB解析式为y=﹣2x+1,AB=2 ![]() ,
,
设点Q(m,0),P(n,n2﹣2n)
∵以A、B、P、Q为顶点的四边形是平行四边形,
①当AB为对角线时,根据中点坐标公式得,则有  ,解得
,解得 ![]() 或
或 ![]()
∴P(1+ ![]() ,2)和(1﹣
,2)和(1﹣ ![]() ,2)
,2)
②当AB为边时,根据中点坐标公式得  解得
解得 ![]() 或
或 ![]()
∴P(1+ ![]() ,4)或(1﹣
,4)或(1﹣ ![]() ,4).
,4).
(3)
解:设T(m,m2﹣2m),∵TM⊥OC,
∴可以设直线TM为y=﹣ ![]() x+b,则m2﹣2m=﹣
x+b,则m2﹣2m=﹣ ![]() m+b,b=m2﹣2m+
m+b,b=m2﹣2m+ ![]() ,
,
由  解得
解得  ,
,
∴OM= ![]() =
= ![]() ,ON=m
,ON=m ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴k= ![]() 时,
时, ![]() =
= ![]() .
.
∴当k= ![]() 时,点T运动的过程中,
时,点T运动的过程中, ![]() 为常数.本题考查二次函数综合题,平行四边形的判定和性质,中点坐标公式等知识,解题
为常数.本题考查二次函数综合题,平行四边形的判定和性质,中点坐标公式等知识,解题
【解析】(1)利用待定系数法即可解决问题(2)①当AB为对角线时,根据中点坐标公式,列出方程组解决问题.②当AB为边时,根据中点坐标公式列出方程组解决问题.(3)设T(m,m2﹣2m),由TM⊥OC,可以设直线TM为y=﹣ ![]() x+b,则m2﹣2m=﹣
x+b,则m2﹣2m=﹣ ![]() m+b,b=m2﹣2m+
m+b,b=m2﹣2m+ ![]() ,求出点M、N坐标,求出OM、ON,根据
,求出点M、N坐标,求出OM、ON,根据 ![]() 列出等式,即可解决问题.本题的关键是利用参数,方程组解决问题,学会转化的思想,属于中考压轴题.
列出等式,即可解决问题.本题的关键是利用参数,方程组解决问题,学会转化的思想,属于中考压轴题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在函数y=
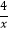 (x>0)的图象上,且OA=4,过点A作AB⊥x轴于点B,则△ABO的周长为 .
(x>0)的图象上,且OA=4,过点A作AB⊥x轴于点B,则△ABO的周长为 . 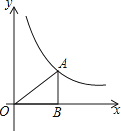
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C是线段AB的中点.
(1)若点D在CB上,且DB=1.5cm,AD=6.5cm,求线段CD的长度.
(2)若将(1)中的“点D在CB上”改为“点D在CB的延长线上”,其它条件不变,请画出相应的示意图,并求出此时线段CD的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.

(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值;
(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.

(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣ ,求⊙O的半径和BF的长.
,求⊙O的半径和BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D.
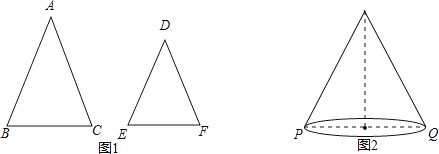
(1)求证: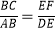 ;
;
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即T(A)= 的对边(底边)/
的对边(底边)/ 的领边(腰)=
的领边(腰)=  ,如T(60°)=1.
,如T(60°)=1.
①理解巩固:T(90°)= , T(120°)= , 若α是等腰三角形的顶角,则T(α)的取值范围是;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1).
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
相关试题

