【题目】如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.
(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣ ![]() ,求⊙O的半径和BF的长.
,求⊙O的半径和BF的长.
参考答案:
【答案】
(1)
解:△ABC是等腰三角形,理由是:如图1,
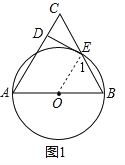
连接OE,
∵DE是⊙O的切线,
∴OE⊥DE,
∵ED⊥AC,
∴AC∥OE,
∴∠1=∠C,
∵OB=OE,
∴∠1=∠B,
∴∠B=∠C,
∴△ABC是等腰三角形
(2)
解:如图2,
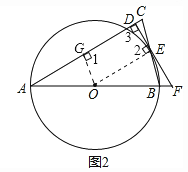
过点O作OG⊥AC,垂足为G,则得四边形OGDE是矩形,
∵△ABC是等腰三角形,
∴∠B=∠C=75°,
∴∠A=180°﹣75°﹣75°=30°,
设OG=x,则OA=OB=OE=2x,AG= ![]() x,
x,
∴DG=0E=2x,
根据AC=AB得:4x= ![]() x+2x+2﹣
x+2x+2﹣ ![]() ,
,
x=1,
∴0E=OB=2,
在直角△OEF中,∠EOF=∠A=30°,
cos30= ![]() ,OF=
,OF= ![]() =2÷
=2÷ ![]() =
= ![]() ,
,
∴BF= ![]() ﹣2,⊙O的半径为2
﹣2,⊙O的半径为2
【解析】(1)连接OE,根据切线性质得OE⊥DE,与已知中的ED⊥AC得平行,由此得∠1=∠C,再根据同圆的半径相等得∠1=∠B,可得出三角形为等腰三角形;(2)通过作辅助线构建矩形OGDE,再设与半径有关系的边OG=x,通过AB=AC列等量关系式,可求得结论.本题考查了切线的性质,由定理可知,若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系,由此得出平行和角的关系,根据两个角相等的三角形是等腰三角形可得△ABC是等腰三角形;第二问运用了直角三角形30°角的性质及等腰三角形和矩形的有关性质,关键是找出恰当的等量关系式:AC=AB,设未知数,列关于x的一元一次方程得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C是线段AB的中点.
(1)若点D在CB上,且DB=1.5cm,AD=6.5cm,求线段CD的长度.
(2)若将(1)中的“点D在CB上”改为“点D在CB的延长线上”,其它条件不变,请画出相应的示意图,并求出此时线段CD的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.

(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中,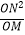 为常数,试确定k的值.
为常数,试确定k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.

(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值;
(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D.
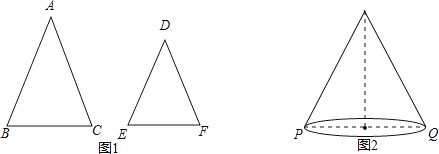
(1)求证: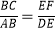 ;
;
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即T(A)= 的对边(底边)/
的对边(底边)/ 的领边(腰)=
的领边(腰)=  ,如T(60°)=1.
,如T(60°)=1.
①理解巩固:T(90°)= , T(120°)= , 若α是等腰三角形的顶角,则T(α)的取值范围是;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1).
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68) -
科目: 来源: 题型:
查看答案和解析>>【题目】动车的开通为扬州市民的出行带来了方便.从扬州到合肥,路程为360km,某趟动车的平均速度比普通列车快50%,所需时间比普通列车少1小时,求该趟动车的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.

(1)求证:四边形AECF是平行四边形;
(2)若AB=6,AC=10,求四边形AECF的面积.
相关试题

