【题目】某中学计划购买A型和B型课桌凳共200套.经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,且购买4套A型和5套B型课桌凳共需1820元.
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
参考答案:
【答案】(1) 购买一套A型课桌凳和一套B型课桌凳各需180元和220元.
(2) 共有3种方案,总费用最低方案是购买A型80套,购买B型120套
【解析】试题分析: (1)根据购买一套A型课桌凳比购买一套B型课桌凳少用40元,以及购买4套A型和5套B型课桌凳共需1820元,得出等式方程求出即可;
(2)利用要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的![]() ,得出不等式组,求出a的值即可,再利用一次函数的增减性得出答案即可.
,得出不等式组,求出a的值即可,再利用一次函数的增减性得出答案即可.
试题解析:
(1)设A型每套![]() 元,B型每套(
元,B型每套(![]() )元
)元
∴![]()
∴![]()
即购买一套A型课桌凳和一套B型课桌凳各需180元和220元。
(2)设A型课桌凳![]() 套,则购买B型课桌凳(
套,则购买B型课桌凳(![]() )套
)套
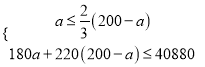
解得![]()
∵![]() 为整数,所以
为整数,所以![]() =78,79,80
=78,79,80
所以共有3种方案。
当a=78时,180a+220(200—a )= 40880
当a=79时,180a+220(200—a )= 40840
当a=80时,180a+220(200—a )= 40800总费用最低,此时200- ![]() =120
=120
即总费用最低方案是购买A型80套,购买B型120套。
-
科目: 来源: 题型:
查看答案和解析>>【题目】1纳米=0.000 000 001米,则2.5纳米应表示为 ( )
A. 2.5×10-8米 B. 2.5×10-9米 C. 2.5×10-10米 D. 2.5×109米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为6cm的⊙O中,点A是劣弧
 的中点,点D是优弧
的中点,点D是优弧 上一点,且∠D=30°,下列四个结论:
上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=6
 cm;③sin∠AOB=
cm;③sin∠AOB=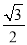 ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.其中正确结论的序号是( )

A. ①③ B. ①②③④ C. ②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为( )

A.6 B.12 C.2
 D.4
D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:
①abc<0;②b<a+c;③4a+2b+c>0;④b2-4ac>0
其中正确结论的有( )
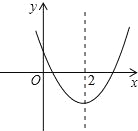
A.①②③ B.①②④ C.①③④ D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形的面积为x2-2xy+x , 长是x , 则这个长方形的宽是( )
A.x-2y
B.x+2y
C.x-2y-1
D.x-2y+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】若两个自然数之积为偶数,则这两个数_____.
相关试题

