【题目】用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:

(1)a= ,b= ,c= ;
(2)这个几何体最少由 个小立方体搭成,最多由 个小立方体搭成;
(3)当d=2,e=1,f=2时,画出这个几何体的左视图.
参考答案:
【答案】(1)a=3,b=1,c=1;
(2)这个几何体最少由9个小立方体搭成,最多由11个小立方体搭成;
(3) 左视图如图:

【解析】试题分析:(1)如图从主视图第三列可看出这一列最高的是由三个立方体搭成,再结合俯视图,第三列仅第一行有立方体,所以a=3;从俯视图可看出第二列的第一行、第二行均有立方体,从主视图看出第二列仅一个立方体,则说明b=c=1;(2)从俯视图可看出第一列的第一、二、三行均有立方体,从主视图上看出第一列最高的有两个立方体,则说明可能是d=2,e=f=1或e=2,d=f=1也可能是f=2,e=d=1,也有可能是d=e=f=2,或者e=d=2,f=1、e=f=2,d=1或者d=f=2,e=1;所以最少有3+1+1+1+1+2=9个立方体,最多有3+1+1+6=11个立方体.
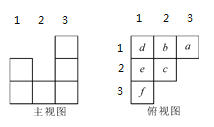
试题解析:(1)如图所示:结合主视图与俯视图可以得到a=3,b=1,c=1.
(2)从主视图和俯视图中可以看出d、e、f中最大为2,所以有以下几种情况:
① d=2,e=f=1② e=2,d=f=1③ f=2,e=d=1,④ e=d=2,f=1⑤ e=f=2,d=1⑥ d=f=2,e=1⑦ d=e=f=2,所以当d、e、f中有一个为2,其他两个为1时,组成几何体的立方体最少为3+1+1+1+1+2=9;当d=e=f=2时,组成几何体的立方体最多为3+1+1+6=11(3)左视图如图所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点p(5,﹣3)关于原点对称的点的坐标是( )
A.(3,﹣5)
B.(﹣5,﹣3)
C.(﹣5,3)
D.(﹣3,5) -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O,P,A三点,点E是正方形内的抛物线上的动点.
(1)建立适当的平面直角坐标系.
①直接写出O,P,A三点坐标;
②求抛物线L的表达式;
(2)求△OAE与△OCE面积之和的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
(1)求这条抛物线的表达式;
(2)连接AB、BC、CD、DA,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图的名称;

视图 视图
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 1的平方根是1
B. ﹣1平方根是﹣1
C. 0的平方根是0
D. 0.01是0.1的一个平方根
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2-4x+3.
(1)该函数与x轴的交点坐标 ;
(2)在平面直角坐标系中,用描点法画出该二次函数的图象;
x
…
0
1
2
3
4
…
y
…
3
0
-1
0
3
…
(3)根据图象回答:
①当自变量x的取值范围满足什么条件时,y<0?
②当0≤x<3时,y的取值范围是多少?
相关试题

