【题目】如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=![]() (x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(1)求k,并用t表示h;
(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.

参考答案:
【答案】(1)k=18,h=5t2;(2)x=5t+1,y=﹣5t2+18,y=![]() ,当y=13时,运动员在与正下方滑道的竖直距离是10米;(3)t=1.8,v乙>7.5
,当y=13时,运动员在与正下方滑道的竖直距离是10米;(3)t=1.8,v乙>7.5
【解析】(1)用待定系数法解题即可;
(2)根据题意,分别用t表示x、y,再用代入消元法得出y与x之间的关系式;
(3)求出甲距x轴1.8米时的横坐标,根据题意求出乙位于甲右侧超过4.5米的v乙.
(1)由题意,点A(1,18)代入y=![]() ,
,
得:18=![]() ,
,
∴k=18,
设h=at2,把t=1,h=5代入,
∴a=5,
∴h=5t2;
(2)∵v=5,AB=1,
∴x=5t+1,
∵h=5t2,OB=18,
∴y=﹣5t2+18,
由x=5t+1,
则t=![]() (x-1),
(x-1),
∴y=﹣![]() (x-1)2+18=
(x-1)2+18=![]() ,
,
当y=13时,13=﹣![]() (x-1)2+18,
(x-1)2+18,
解得x=6或﹣4,
∵x≥1,
∴x=6,
把x=6代入y=![]() ,
,
y=3,
∴运动员在与正下方滑道的竖直距离是13﹣3=10(米);
(3)把y=1.8代入y=﹣5t2+18
得t2=![]() ,
,
解得t=1.8或﹣1.8(负值舍去)
∴x=10
∴甲坐标为(10,1.8)恰号落在滑道y=![]() 上,
上,
此时,乙的坐标为(1+1.8v乙,1.8),
由题意:1+1.8v乙﹣(1+5×1.8)>4.5,
∴v乙>7.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形 对.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=
 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=
 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】黑白两种颜色的正方形纸片,按如图所示的规律拼成若干个图案:

第4个图案中有白色纸片________块,第n个图案中有白色纸片________块。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,连结AE、DE、DC,且AE=CD.

(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一直线上.
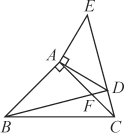
(1)求证:△BAD≌△CAE;
(2)猜想BD,CE有何特殊位置关系,并说明理由.
-
科目: 来源: 题型:
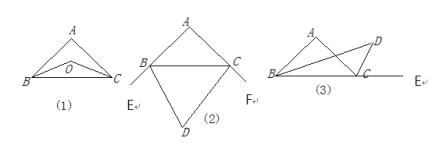
查看答案和解析>>【题目】(1)如图⑴,在△ABC中,∠ABC 、∠ACB的平分线相交于点O,试说明∠BOC=90°+
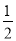 ∠A;
∠A;(2)如图⑵,在△ABC中,BD、CD分别是∠ABC 、∠ACB的外角平分线,试说明∠D=90°-
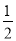 ∠A;
∠A;(3)如图⑶,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D,试说明∠A=2∠D。
相关试题

