【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:①AC=AD;②BD⊥AC;③四边形ACED是菱形.其中正确的个数是( )

A.0 B.1 C.2 D.3
参考答案:
【答案】D
【解析】
试题分析:根据旋转和等边三角形的性质得出∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE,求出△ACD是等边三角形,求出AD=AC,根据菱形的判定得出四边形ABCD和ACED都是菱形,根据菱形的判定推出AC⊥BD. ∵将等边△ABC绕点C顺时针旋转120°得到△EDC, ∴∠ACE=120°,∠DCE=∠BCA=60°,AC=CD=DE=CE, ∴∠ACD=120°﹣60°=60°, ∴△ACD是等边三角形,
∴AC=AD,AC=AD=DE=CE, ∴四边形ACED是菱形,
∵将等边△ABC绕点C顺时针旋转120°得到△EDC,AC=AD, ∴AB=BC=CD=AD,
∴四边形ABCD是菱形, ∴BD⊥AC,∴①②③都正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行“社会主义核心价值观”演讲比赛,学校对30名参赛选手的成绩进行了分组统计,结果如下表:
分数x(分)
4≤x<5
5≤x<6
6≤x<7
7≤x<8
8≤x<9
9≤x<10
频数
2
6
8
5
5
4
由上可知,参赛选手分数的中位数所在的分数段为( )
A. 5≤x<6B. 6≤x<7C. 7≤x<8D. 8≤x<9
-
科目: 来源: 题型:
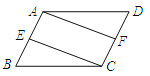
查看答案和解析>>【题目】如图,在□ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
(1)求证:△BEC≌△DFA;
(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市开展“阳光”活动中,为解中学生活动开展情况,随机抽查全市八年级部分同学1分钟,将抽查结果进行,并绘制两个不完整图.请根据图中提供信息,解答问题:

(1)本次共抽查多少名学生?
(2)请补全直方图空缺部分,直接写扇形图中范围135≤x<155所在扇形圆心角度数.
(3)若本次抽查中,在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生成绩为优秀?
(4)请你根据以上信息,对我市开展学生活动谈谈自己看法或建议 -
科目: 来源: 题型:
查看答案和解析>>【题目】太阳半径约为696000km,将696000用科学记数法表示为( )
A. 696×103B. 69.6×104C. 0.696×106D. 6.96×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.

-
科目: 来源: 题型:
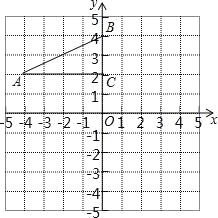
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣4,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
相关试题

