【题目】如图,已知l1⊥l2 , ⊙O与l1 , l2都相切,⊙O的半径为2cm.矩形ABCD的边AD,AB分别与l1 , l2重合,AB=4 ![]() cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s). 
(1)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1 , A1 , C1恰好在同一直线上,则移动时间t= .
(2)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm).当d<2时,求t的取值范围 .
参考答案:
【答案】
(1)2+ ![]()
(2)2﹣ ![]()
![]() <t<2+2
<t<2+2 ![]()
【解析】解:(1.)连接OO1 , 并延长交l2于点E,如图1, 
过点O1作O1F⊥l1于点F,
∴由题意知:OO1=3t,AA1=4t,
∵tan∠DAC= ![]() ,
,
∴∠DAC=60°,
∴tan∠O1A1F= ![]() ,
,
∴A1F= ![]()
![]() ,
,
∵AA1﹣A1F=O1E,
∴4t﹣ ![]()
![]() =3t+2,
=3t+2,
∴t=2+ ![]() ;
;
(2.)当d=2时,
此时⊙O与直线AC相切,
当直线AC在⊙O的左边,如图2,
由(1)可知,A1F= ![]()
![]() ,
,
∴AA1+A1F=O1E,
∴4t+ ![]()
![]() =3t+2,
=3t+2,
∴t=2﹣ ![]()
![]() ,
,
当直线AC在⊙O的右边,如图3,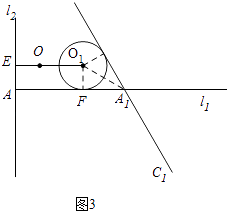
此时,A1F=2 ![]()
∴AA1﹣A1F=O1E,
∴4t﹣2 ![]() =3t+2,
=3t+2,
∴t=2+2 ![]() ,
,
综上所述,当d<2时,t的取值范围为:2﹣ ![]()
![]() <t<2+2
<t<2+2 ![]() .
.
所以答案是:(1)2+ ![]() ;(2)2﹣
;(2)2﹣ ![]()
![]() <t<2+2
<t<2+2 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
 给出下列结论:①
给出下列结论:① 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4-a的解;④x,y都为自然数的解有4对.其中正确的个数为( )
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4-a的解;④x,y都为自然数的解有4对.其中正确的个数为( )A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是小红在某个路口统计20分钟各种车辆通过情况制成的统计表,其中空格处的字迹已模糊,但小红还记得7:50~8:00时段内的电瓶车车辆数与8:00~8:10时段内的货车车辆数之比是7∶2.
电瓶车
公交车
货车
小轿车
合计
7:50~8:00
5
63
133
8:00~8:10
5
45
82
合计
67
30
108
(1)若在7:50~8:00时段,经过的小轿车数量正好是电瓶车数量的
 ,求这个时段内的电瓶车通过的车辆数;
,求这个时段内的电瓶车通过的车辆数;(2)根据上述表格数据,求在7:50~8:00和8:00~8:10两个时段内电瓶车和货车的车辆数;
(3)据估计,在所调查的7:50~8:00时段内,每增加1辆公交车,可减少8辆小轿车行驶,为了使该时段内小轿车流量减少到比公交车多13辆,则在该路口应再增加几辆公交车?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线y=
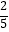 x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.
x+2与x轴交于点A,与y轴交于点C,抛物线y=ax2+4ax+b经过A.C两点,且与x轴交于另一点B.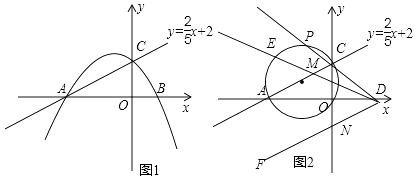
(1)求抛物线的解析式;
(2)若点Q在抛物线上,且△AQC与△BQC面积相等,求点Q的坐标;
(3)如图2,P为△AOC外接圆上弧ACO的中点,直线PC交x轴于点D,∠EDF=∠ACO,当∠EDF绕点D旋转时,DE交直线AC于点M,DF交y轴负半轴于点N.请你探究:CN﹣CM的值是否发生变化?若不变,求出其值;若变化,求出变化范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了发展乡村旅游,洪江村准备在洪江河道上修一座与河道垂直的吊桥,如图1所示,直线l、m代表洪江河的两岸,且l∥m,点A是洪江村自助农场的所在地,点B是洪江村游乐园所在地.
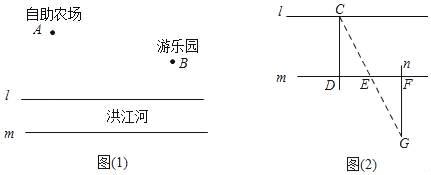
问题1:吊桥的选址
吊桥准备选在到A、B两地的距离之和刚好为最小的点C处,即在直线l上找到使(AC+BC)的值为最小的点C的位置.请利用你所学的知识帮助村委会设计选址方案(直接在图1里作图),并简单说明你所设计方案的原理
问题2:河道的宽度
在测量河道的宽度时,施工队在河道南侧的开阔地用以下方法(如图2所示):①作CD⊥1,与河对岸的直线m相交于D;②在直线m上取E、F两点,使得DE=EF=10米;③过点F作m的垂线n;④在直线n上找到一点G,使得点G与C、E两点在同一直线上;⑤测量FG的长度为20米.请问你知道河道的宽度吗?说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】七(1)班小明同学通过《测量硬币的厚度与质量》实验得到了每枚硬币的厚度和质量,数据如下表.他从储蓄罐取出一把5角和1元硬币,为了知道总的金额,他把这些硬币叠起来,用尺量出它们的总厚度为22.6mm,又用天平称出总质量为78.5g,请你帮助小明同学算出这把硬币的总金额为______元.
1元硬币
5角硬币
每枚厚度(单位:mm)
1.8
1.7
每枚质量(单位:g)
6.1
6.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了对一颗倾斜的古杉树AB进行保护,需测量其长度:在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,(参考数据:
 ≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( )
≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( ) 
A.7.27
B.16.70
C.17.70
D.18.18
相关试题

