搜索
【题目】把下列的推理过程补充完整，并在括号里填上推理的依据：
如图，∠E=∠1，∠3+∠ABC=180°，BE是∠ABC的角平分线．
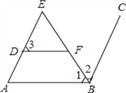
试说明：DF∥AB
解：因为BE是∠ABC的角平分线
所以 （角平分线的定义）
又因为∠E=∠1（已知）
所以∠E=∠2（ ）
所以 （ ）
所以∠A+∠ABC=180°（ ）
又因为∠3+∠ABC=180°（已知）
所以 （ ）
所以DF∥AB（ ）
参考答案：
【答案】答案见解析.
【解析】试题分析：根据题意、结合图形，根据平行线的判定定理和性质定理解答即可．
试题解析：因为BE是∠ABC的角平分线，
所以∠1=∠2（角平分线的定义），
又因为∠E=∠1（已知）
所以∠E=∠2（等量代换）
所以AE∥BC（内错角相等，两直线平行）
所以∠A+∠ABC=180°（两直线平行，同旁内角互补）
又因为∠3+∠ABC=180°（已知）
所以∠3=∠A（同角的补角相等）
所以DF∥AB（同位角相等，两直线平行）．
-
科目： 来源： 题型：
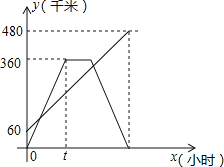
查看答案和解析>>【题目】甲、乙两车分别从相距480km的A、B两地相向而行，乙车比甲车先出发1小时，并以各自的速度匀速行驶，途径C地，甲车到达C地停留1小时，因有事按原路原速返回A地．乙车从B地直达A地，两车同时到达A地．甲、乙两车距各自出发地的路程y（千米）与甲车出发所用的时间x（小时）的关系如图，结合图象信息解答下列问题：
（1）乙车的速度是 千米/时，t＝ 小时；
（2）求甲车距它出发地的路程y与它出发的时间x的函数关系式，并写出自变量的取值范围；
（3）直接写出乙车出发多长时间两车相距120千米．
-
科目： 来源： 题型：
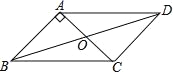
查看答案和解析>>【题目】已知：如图，在ABCD中，对角线AC，BD交于点O，AB⊥AC，AB=1，BC=
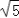．（1）求平行四边形ABCD的面积S□ABCD；
（2）求对角线BD的长．
-
科目： 来源： 题型：
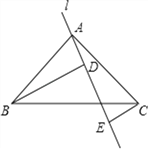
查看答案和解析>>【题目】如图，Rt△ABC中，AB=AC，∠BAC=90°，直线l为经过点A的任一直线，BD⊥l于D，CE⊥AE，若BD＞CE，试问：
（1）AD与CE的大小关系如何？请说明理由；
（2）线段BD，DE，CE之间的数量之间关系如何？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，点P的坐标为（
，
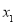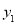），点Q的坐标为（
，
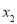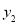），且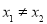
，
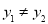，若P，Q为某个矩形的两个顶点，且该矩形的边均与某条坐标轴垂直，则称该矩形为点P，Q的“相关矩形”．下图为点P，Q 的“相关矩形”的示意图．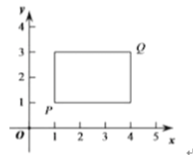
（1）已知点A的坐标为（1，0）．
①若点B的坐标为（3，1）求点A，B的“相关矩形”的面积；
②点C在直线x=3上，若点A，C的“相关矩形”为正方形，求直线AC的表达式；
（2）⊙O的半径为
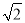，点M的坐标为（m，3）．若在⊙O上存在一点N，使得点M，N的“相关矩形”为正方形，求m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】（x+k）2=x2+2kx+4，则k的值是（）
A.﹣2
B.2
C.±2
D.3 -
科目： 来源： 题型：
查看答案和解析>>【题目】4的平方根是（ ）
A. ﹣2 B. 2 C. ±2 D. 16
相关试题
