【题目】在平面直角坐标系xOy中,点P的坐标为(![]() ,
,![]() ),点Q的坐标为(
),点Q的坐标为(![]() ,
,![]() ),且
),且![]() ,
,![]() ,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
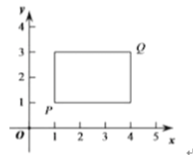
(1)已知点A的坐标为(1,0).
①若点B的坐标为(3,1)求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为![]() ,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
参考答案:
【答案】(1)①2;②![]() 或
或 ![]() ;(2)1≤m≤5 或者
;(2)1≤m≤5 或者![]() .
.
【解析】
试题分析:(1)①易得S=2;
②得到C的坐标可以为(3,2)或者(3,-2),设AC的表达式为y=kx+b,将A、C分别代入AC的表达式即可得出结论;
(2)若⊙O上存在点N,使MN的相关矩形为正方形,则直线MN的斜率k=±1,即过M点作k=±1的直线,与⊙O相切,求出M的坐标,即可得出结论.
试题解析:(1)①S=2×1=2;
②C的坐标可以为(3,2)或者(3,-2),设AC的表达式为y=kx+b,将A、C分别代入AC的表达式得到:![]() 或
或![]() ,解得:
,解得:![]() 或
或![]() ,则直线AC的表达式为
,则直线AC的表达式为![]() 或
或 ![]() ;
;
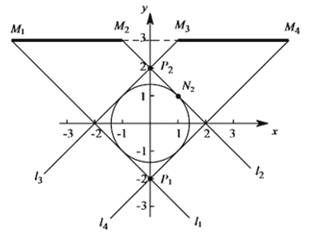
(2)若⊙O上存在点N,使MN的相关矩形为正方形,则直线MN的斜率k=±1,即过M点作k=±1的直线,与⊙O有交点,即存在N,当k=-1时,极限位置是直线与⊙O相切,如图![]() 与
与![]() ,直线
,直线![]() 与⊙O切于点N,ON=
与⊙O切于点N,ON=![]() ,∠ONM=90°,∴
,∠ONM=90°,∴![]() 与y交于
与y交于![]() (0,-2).
(0,-2).![]() (
(![]() ,3),∴
,3),∴![]() ,∴
,∴![]() =-5,∴
=-5,∴![]() (-5,3);同理可得
(-5,3);同理可得![]() (-1,3);
(-1,3);
当k=1时,极限位置是直线![]() 与
与![]() (与⊙O相切),可得
(与⊙O相切),可得![]() (1,3),
(1,3), ![]() (5,3).
(5,3).
因此m的取值范围为1≤m≤5 或者![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,对角线AC,BD交于点O,AB⊥AC,AB=1,BC=
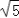 .
.(1)求平行四边形ABCD的面积S□ABCD;
(2)求对角线BD的长.
-
科目: 来源: 题型:
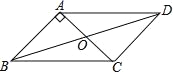
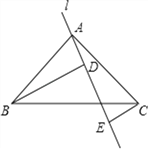
查看答案和解析>>【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列的推理过程补充完整,并在括号里填上推理的依据:
如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.
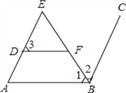
试说明:DF∥AB
解:因为BE是∠ABC的角平分线
所以 (角平分线的定义)
又因为∠E=∠1(已知)
所以∠E=∠2( )
所以 ( )
所以∠A+∠ABC=180°( )
又因为∠3+∠ABC=180°(已知)
所以 ( )
所以DF∥AB( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】(x+k)2=x2+2kx+4,则k的值是()
A.﹣2
B.2
C.±2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】4的平方根是( )
A. ﹣2 B. 2 C. ±2 D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】去年长春财政用于“三农”的支出达到33900万元,这一支出用科学记数法可表示为________万元 .
相关试题

