【题目】某花卉种植基地欲购进甲、乙两种君子兰进行培育。若购进甲种2株,乙种3株,则共需成本l700元;若购进甲种3株,乙种l株.则共需成本l500元。
(1)求甲、乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购入甲、乙两种君子兰,若购入乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
参考答案:
【答案】(1)400元;300元;(2)20株.
【解析】试题分析:(1)设甲种君子兰每株成本为x元,乙种君子兰每株成本为y元.此问中的等量关系:①购进甲种2株,乙种3株,则共需要成本1700元;②购进甲种3株,乙种1株,则共需要成本1500元;依此列出方程组求解即可;
(2)结合(1)中求得的结果,根据题目中的不等关系:成本不超过30000元,列不等式进行求解.
解:(1)设甲种君子兰每株成本为x元,乙种君子兰每株成本为y元,依题意有
![]()
解得![]()
故甲种君子兰每株成本为400元,乙种君子兰每株成本为300元.
(2)设购进甲种君子兰a株,则购进乙种君子兰(3a+10)株,依题意有
400a+300(3a+10)≤30000,
解得a≤![]()
∵a为整数
∴a最大为20.
故最多购进甲种君子兰20株.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2;以此下去…,则正方形A4B4C4D4的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) ×
×  ÷
÷ 
(2)( )+(
)+(  )
)
(3) +6
+6 
(4)(2 ﹣3
﹣3  )÷
)÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;

(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,若点P在第四象限,且点P到x轴的距离为1,到y轴的距离为3,则点的坐标为( )
A. (3,-1)B. (-3,1)C. (1,-3)D. (-1,3)
-
科目: 来源: 题型:
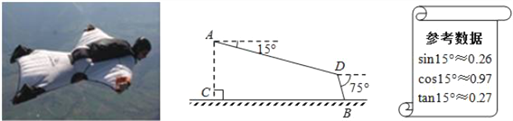
查看答案和解析>>【题目】如图,某翼装飞行员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离BC(结果精确到1m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形ABC中任意一点P(x0,y0)经平移后対应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1,若A(﹣2,3),则A1的坐标为_____.
相关试题

