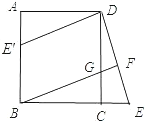
【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.

(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由.
参考答案:
【答案】(1)见解析;(2)四边形E′BGD是平行四边形,理由见解析.
【解析】
试题分析:(1)由正方形ABCD,得BC=CD,∠BCD=∠DCE=90°,又CG=CE,所以△BCG≌△DCE(SAS).
(2)由(1)得BG=DE,又由旋转的性质知AE′=CE=CG,所以BE′=DG,从而证得四边形E′BGD为平行四边形.
(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°.
∵∠BCD+∠DCE=180°,
∴∠BCD=∠DCE=90°.
又∵CG=CE,
∴△BCG≌△DCE.
(2)解:四边形E′BGD是平行四边形.理由如下:
∵△DCE绕D顺时针旋转90°得到△DAE′,
∴CE=AE′.
∵CE=CG,
∴CG=AE′.
∵四边形ABCD是正方形,
∴BE′∥DG,AB=CD.
∴AB﹣AE′=CD﹣CG.
即BE′=DG.
∴四边形E′BGD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.
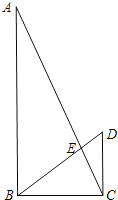
(1)求BE的长度;
(2)求△ABE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣2x+m=0总有实数根,则m应满足的条件是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】当1≤x≤2时,ax+2>0,则a的取值范围是( )
A.a>﹣1 B.a>﹣2
C.a>0 D.a>﹣1且a≠0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A从点(1,0)出发,以1个单位长度/秒的速度沿x轴向正方向运动,以O、A为顶点作菱形OABC,使点B、C在第一象限内,且∠AOC=60°,点P的坐标为(0,3),设点A运动了t秒,求:
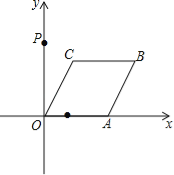
(1)点C的坐标(用含t的代数式表示);
(2)点A在运动过程中,当t为何值时,使得△OCP为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(2x-3)(5-2x)=ax2+bx+c,则a+b+c=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ax·ay=a5,ax÷ay=a,求x2-y2的值.
相关试题

