【题目】如图①,(1)已知∠ABC,射线ED∥AB,过点E作∠DEF=∠ABC,试说明BC∥EF;
(2)如图②,已知∠ABC,射线ED∥AB,∠ABC+∠DEF=180°.判断直线BC与直线EF的位置关系,并说明理由;
(3)根据以上探究,你发现了一个什么结论?请你写出来;
(4)如图③,已知AC⊥BC,CD⊥AB,DE⊥AC,HF⊥AB,若∠1=48°,试求∠2的度数.



参考答案:
【答案】(1)(2)(3)见解析;(4)132°.
【解析】试题分析:(1)根据平行线的判定和性质即可得到结论;
(2)根据平行线的判定和性质即可得到结论;
(3)由(1)、(2)的结论即可得到结果;
(4)根据平行线的判定和性质即可得到结论.
试题解析:
(1)∵ED∥AB,
∴∠B=∠DOC,
∵∠DEF=∠ABC,
∴∠DOC=∠DEF,
∴BC∥EF;
(2)∵ED∥AB,
∴∠B=∠BOE,
∵∠ABC+∠DEF=180°,
∴∠BOE+∠DEF=180°,
∴BC∥EF;
(3)由(1)、(2)可得,如果两个角相等或互补且一边平行,则另一边也平行;
(4)∵AC⊥BC,DE⊥AC,
∴DE∥BC,
∴∠DCB=∠1=48°,
∵CD⊥AB,HF⊥AB,
∴CD∥HF,
∴∠2=180°-∠DCB=132°.
-
科目: 来源: 题型:
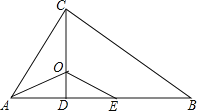
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC。
(1)求证:△AOC≌△A0E;
(2)求证:OE∥BC。
-
科目: 来源: 题型:
查看答案和解析>>【题目】图(1)是我们常见的“箭头图”,其中隐藏着哪些数学知识呢?下面请你解决以下问题:

(1)观察如图(1)“箭头图”,试探究∠BDC与∠A、∠B、∠C之间大小的关系,并说明理由;
(2)请你直接利用以上结论,回答下列两个问题:
①如图(2),把一块三角板XYZ放置在△ABC上,使其两条直角边XY、XZ恰好经过点B、C.若∠A=50°,则∠ABX+∠ACX= ;
②如图(3),∠ABD,∠ACD的五等分线分别相交于点G1、G2、G3、G4,若∠BDC=135°,∠BG1C=67°,求∠A的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )

A. (6,0) B. (6,3) C. (6,5) D. (4,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )
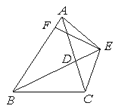
A.①②③ B.①③④ C.①②④ D.①②③④
-
科目: 来源: 题型:
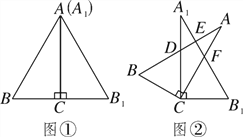
查看答案和解析>>【题目】将两块相同的含30°角的直角三角板按图①的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图②的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
(1)当旋转角等于20°时,∠BCB1=________度;
(2)当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
相关试题

