【题目】如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE.
(1)如图1,若AB=![]() ,BE=5,求AE的长;
,BE=5,求AE的长;
(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC.

参考答案:
【答案】(1)1;(2)证明见解析.
【解析】
试题分析:(1)根据等腰直角三角形的性质得到AC=BC=![]() AB=4,根据勾股定理得到CE=
AB=4,根据勾股定理得到CE=![]() =3,于是得到结论;
=3,于是得到结论;
(2)根据等腰直角三角形的性质得到∠CAB=45°,由于∠AFB=∠ACB=90°,推出A,F,C,B四点共圆,根据圆周角定理得到∠CFB=∠CAB=45°,求得∠DFC=∠AFC=135°,根据全等三角形的性质即可得到结论.
试题解析:(1)∵∠ACB=90°,AC=BC,∴AC=BC=![]() AB=4,∵BE=5,∴CE=
AB=4,∵BE=5,∴CE=![]() =3,∴AE=4﹣3=1;
=3,∴AE=4﹣3=1;
(2)∵∠ACB=90°,AC=BC,∴∠CAB=45°,∵AF⊥BD,∴∠AFB=∠ACB=90°,∴A,F,C,B四点共圆,∴∠CFB=∠CAB=45°,∴∠DFC=∠AFC=135°,在△ACF与△DCF中,∵AF=DF,∠AFC=∠DFC,CF=CF,∴△ACF≌△DCF,∴CD=AC,∵AC=BC,∴AC=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:-24-2×(-3)+|-2-5|-(-1)2019
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=
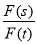 ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式由左边到右边的变形中,属于分解因式的是( )
A.a(x+y)=ax+ay
B.x2﹣4x+4=x(x﹣4)+4
C.10x2﹣5x=5x(2x﹣1)
D.x2﹣16+6x=(x+4)(x﹣4)+6x -
科目: 来源: 题型:
查看答案和解析>>【题目】支付宝与“快的打车”联合推出优惠,“快的打车”一夜之间红遍大江南北.据统计,2016年“快的打车”账户流水总金额达到147.3亿用科学记数法表示为( )
A.1.473×1010
B.14.73×1010
C.1.473×1011
D.1.473×1012 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小张两人练习电脑打字,小明每分钟比小张少打6个字,小明打120个字所用的时间和小张打180个字所用的时间相等.求小明和小张每分钟各打多少个字?
-
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究与应用:
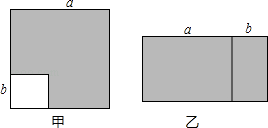
(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是(写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 , 宽是 , 面积是(写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式(用式子表达)
(4)运用你所得到的公式计算:10.3×9.7.
相关试题

