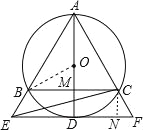
【题目】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F;
(1)求证:EF与⊙O相切;
(2)若BC=2![]() ,MD=
,MD=![]() ,求CE的长.
,求CE的长.

参考答案:
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)根据垂径定理证得AD⊥BC,然后根据平行线的性质证得AD⊥EF,即可证得结论;
(2)连接OB,根据勾股定理求得OB和OM,由BC∥EF,证得△ABC∽△AEF,根据相似三角形的性质求得EF的长,解直角三角形ACM求得∠CAM=30°,进而求得CN的长和∠FCN=∠CAM=30°,解直角三角形求得NF,得出EN,然后根据勾股定理即可求得.
试题解析:(1)∵AD是⊙O的直径,AD与BC相交于点M,且BM=MC,
∴AD⊥BC,
∵EF∥BC,
∴AD⊥EF,
∴EF与⊙O相切;
(2)连接OB,
在△OBM中,BM2+OM2=OB,即(![]() )+(OB﹣
)+(OB﹣![]() )=OB2,OB=2
)=OB2,OB=2![]()
∴OM=MD=![]() ,
,
∵BC∥EF,
∴△ABC∽△AEF
∴![]() ,
,
∴EF=![]() ,
,
∵tan∠CAM=![]() ,
,
∴∠CAM=30°,
作CN⊥EF,
∵AD⊥EF,
∴CN∥AD,
∴∠FCN=∠CAM=30°,
∵BC∥EF,
∴四边形MDNC是矩形,
∴CN=MD=![]() ,
,
∴NF=CNtan30°=![]() ×
×![]() =
=![]() ,
,
∴EN=EF﹣NF=![]() ﹣
﹣![]() =
=![]() ,
,
∴EC=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承优秀传统文化,某校团委组织了一次全校3 000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
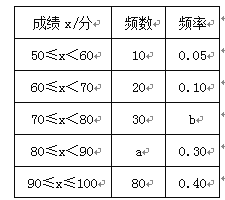
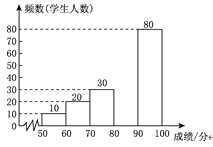
请根据所给信息,解答下列问题:
(1)a=________,b=________;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3 000名学生中成绩为“优”等的大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正比例函数y=(k-3)x的图象经过一、三象限,那么k的取值范围是( )
A. k>0 B. k>3 C. k<0 D. k<3
-
科目: 来源: 题型:
查看答案和解析>>【题目】我区约有2930名学生参加本次模拟考试,这个数据用科学记数法可以表示为____.
(精确到百位)
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出如下5种图形:①矩形,②等边三角形,③正五边形,④圆,⑤线段.其中,是轴对称图形但不是中心对称图形的有____.(请将所有符合题意的序号填在横线上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为﹣10,B点对应的数为70
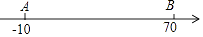
(1)请写出AB的中点M对应的数
(2)现在有一只电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2个单位/秒的速度向左运动,设两只电子蚂蚁在数轴上的C点相遇,请你求出C点对应的数
(3)若当电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2单位/秒的速度向左运动,经过多长时间两只电子蚂蚁在数轴上相距35个单位长度,并写出此时P点对应的数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=5,AB=8,求
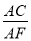 的值.
的值.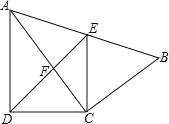
相关试题

