【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,则图3中共有7个正方形;……如此剪下去,则第n个图形中正方形的个数是多少?

(1)将下表填写完整:
图(n) | 1 | 2 | 3 | 4 | 5 | …… | n |
正方形的个数 | 1 | 4 | 7 | …… | an |
(2)an= (用含n的代数式表示)
(3)按照上述方法,能否得到2019个正方形?如果能,请求出n;如果不能,请简述理由.
参考答案:
【答案】(1)10,13;(2)3n-2;(3)不能,
【解析】
根据已知图形可以发现:每次剪开,都会增加3个正方形,所以可以得到此题的规律为:第n个图形中的正方形个数为:3n-2.
(1)根据已知图形可以发现:每次剪开,都会增加3个正方形,
∴第4个图中为7+3=10个,第5个图中为10+3=13个;
(2)根据(1)中的数据规律可知:第n个图形中的正方形个数为:![]() ;
;
(3)不能.
∵若能得到2019个正方形,则有![]() ,则
,则![]() ,但是2021不能被3整除,∴不能得到2019个正方形.
,但是2021不能被3整除,∴不能得到2019个正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,点
中,点 、
、 是正方形内两点,
是正方形内两点, ,
, ,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程:
(1)在图1中,连接
 ,且
,且
①求证:
 与
与 互相平分;
互相平分;②求证:
 ;
;(2)在图2中,当
 ,其它条件不变时,
,其它条件不变时, 是否成立?若成立,请证明:若不成立,请说明理由.
是否成立?若成立,请证明:若不成立,请说明理由.
(3)在图3中,当
 ,
, ,
, 时,求
时,求 之长.
之长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E,F分别是AD,BC的中点,连结AF,BE,CE,DF分别交于点M,N,则四边形EMFN是( )

A. 梯形B. 菱形
C. 矩形D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=16cm,BC=22cm,点P从点A出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.

(1)当t为多少时,四边形ABQP成为矩形?
(2)四边形PBQD是否能成为菱形?若能,求出t的值;若不能,请说明理由,并探究如何改变Q点的速度(匀速运动),使四边形PBQD在某一时刻为菱形,求点Q的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a是单项式-xy2的系数,b是最小的正整数,c是多项式2m2n-m3n2-m-2的次数.请回答下列问题:
(1)请直接写出a、b、c的值.a= ,b= ,c= .
(2)数轴上,a、b、c三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点B与点c之间的距离表示为BC,点A与点C之间的距离表示为AC,点A与点C之间的距离表示为AC.
①t秒钟过后,AC的长度为 (用含t的关系式表示);
②请问:BC-AB的值是否会随着时间t的变化而改变?若变化,请说明理由;若不变,请求出其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD向右平移一段距离后得到四边形
 .
.
(1)找出图中存在的平行且相等的四条线段(即四条线段全部互相平行且相等);
(2)找出图中存在的四组相等的角;
(3)四边形ABCD与四边形
 的形状、大小相同吗?为什么?
的形状、大小相同吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
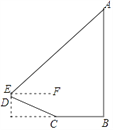
A. 22.5 米 B. 24.0 米 C. 28.0 米 D. 33.3 米
相关试题

