【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“奇巧数”,如12=![]() ,20=
,20=![]() ,28=
,28=![]() ,……,因此12,20,28这三个数都是奇巧数。
,……,因此12,20,28这三个数都是奇巧数。
(1)52,72都是奇巧数吗?为什么?
(2)设两个连续偶数为2n,2n+2(其中n为正整数),由这两个连续偶数构造的奇巧数是8的倍数吗?为什么?
(3)研究发现:任意两个连续“奇巧数”之差是同一个数,请给出验证。
参考答案:
【答案】(1)52是奇巧数,72不是;理由见解析;(2)不是,理由见解析;(3)答案见解析.
【解析】
(1)根据相邻两个偶数的平方差,可得答案;
(2)根据相邻两个偶数的平方差,神秘数的定义,可得答案;
(3)根据相邻两个奇数的平方差,神秘数的定义,可得答案.
(1)52是奇巧数,72不是;因为52=142-122,12,14是连续偶数,所以52是奇巧数;而72不能等于两个连续偶数的平方差,所以72不是奇巧数;
(2)由于![]() ,由于(2n+1)是奇数,不能被2整除,所以由2n,2n+2(其中n为正整数)这两个连续偶数构造的奇巧数不是8的倍数;
,由于(2n+1)是奇数,不能被2整除,所以由2n,2n+2(其中n为正整数)这两个连续偶数构造的奇巧数不是8的倍数;
(3)设n为非负整数,由于![]() =
=![]() =8.
=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养,随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成如图两幅统计图,请你结合图中信息解答问题.
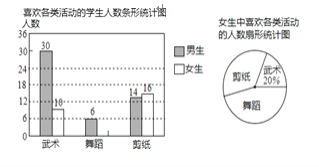
(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是 ;
(3)已知该校有1200名学生,请你根据样本估计全校学生中喜欢剪纸的人数.
-
科目: 来源: 题型:
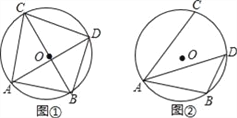
查看答案和解析>>【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在解一元二次方程时,发现有这样一种解法:
如:解方程
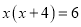 .
.解:原方程可变形,得:
 .
. ,
, ,
, .
.直接开平方并整理,得.
 ,
, 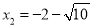 .
.我们称小明这种解法为“平均数法”.
(1)下面是小明用“平均数法”解方程
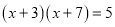 时写的解题过程.
时写的解题过程. 解:原方程可变形,得:
 .
. ,
, .
.直接开平方并整理,得.
 ,
,  .
.上述过程中的a、b、c、d表示的数分别为 , , , .
(2)请用“平均数法”解方程:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=4,∠BAC=120°,AD为BC边上的高,点P从点B以每秒
 个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.
个单位长度的速度向终点C运动,同时点Q从点C以每秒1个单位长度的速度向终点A运动,其中一个点到达终点时,两点同时停止.(1)求BC的长;
(2)设△PDQ的面积为S,点P的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围;
(3)在动点P、Q的运动过程中,是否存在PD=PQ,若存在,求出△PDQ的周长,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为一种新型电子产品在该城市的特约经销商,已知每件产品的进价为40元,该公司每年销售这种产品的其他开支(不含进货价)总计100万元,在销售过程中得知,年销售量y(万件)与销售单价x(元)之间存在如表所示的函数关系,并且发现y是x的一次函数.
销售单价x(元)
50
60
70
80
销售数量y(万件)
5.5
5
4.5
4
(1)求y与x的函数关系式;
(2)问:当销售单价x为何值时,该公司年利润最大?并求出这个最大值;
【备注:年利润=年销售额﹣总进货价﹣其他开支】
(3)若公司希望年利润不低于60万元,请你帮助该公司确定销售单价的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),在△ABC中,∠A=62°,∠ABD=20°,∠ACD=35°,求∠BDC的度数.

(2)图(1)所示的图形中,有点像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”,观察“规形图”图(2),试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由.
(3)请你直接利用以上结论,解决以下问题:
①如图(3),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=42°,则∠ABX+∠ACX= °.
②如图(4),DC平分∠ADB,EC平分∠AEB,若∠DAE=60°,∠DBE=140°,求∠DCE的度数.
③如图(5),∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG1C=68°,求∠A的度数.
相关试题

