【题目】如图,已知矩形ABCD,折叠矩形,点B刚好落在对角线AC上点F处,AD=8,CD=6.求折痕AE的长.

参考答案:
【答案】![]() .
.
【解析】
由题意,△AFE≌△ABE,所以EF=BE,AF=AB=6,∠AFE=∠B=90°,则∠EFC=90,FC=AC-AF=4,设BE=x,则EF=x,CE=8-x.在Rt△CFE中,利用勾股定理求出x,在Rt△ABE中,利用勾股定理求出AE即可.
解:∵ABCD是矩形,
∴∠B=90°,AB=CD=6,BC=AD=8,AC=10,
∵折叠矩形,点B刚好落在对角线AC上点F处,
∴△AFE≌△ABE,
∴EF=BE,AF=AB=6,∠AFE=∠B=90°,
∴∠EFC=90°,FC=AC﹣AF=4,
设BE=x,则EF=x,CE=8﹣x.
在Rt△CFE中,EF2+FC2=EC2,
即x2+42=(8﹣x)2,
解得:x=3,
在Rt△ABE中,AE![]() 3
3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,数轴上标出若干个点,每相邻两点相距一个单位长度,点A,B,C,D对应的数分别是数a,b,c,d,且d-2a=10,那么数轴的原点应是( )

A.点A
B.点B
C.点C
D.点D -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC三个顶点的位置如图所示(每个小正方形的边长均为 1),△ABC中任意一点 P(x,y)平移后的对应点为 P′(x+3,y+2).
(1)将△ABC按此规律平移后得到△A′B′C′请画出平移后的△A′B′C′(其中 A′,B′,C′分别是A,B,C的对应点,不写画法).
(2)直接写出 A′,B′,C′三点的坐标:A′(____,____),B′(____,____),C′(____,____).
(3)求△A′B′C′的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
-
科目: 来源: 题型:
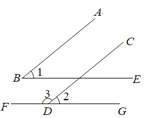
查看答案和解析>>【题目】如图,已知 AB∥CD,BE∥FG.
(1)如果∠1=53°,求∠2和∠3的度数;
(2)本题隐含着一个规律,请你根据(1)的结果进行归纳,如果一个角的两边分别平行于另一个角的两边,那么这两个角__________;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一个角比另一个角的 2倍小 30°,求这两个角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字0所对应的点与数轴上的数﹣2所对应的点重合,再让圆沿着数轴按顺时针方向滚动,那么数轴上的数﹣2016将与圆周上的哪个数字重合( )

A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
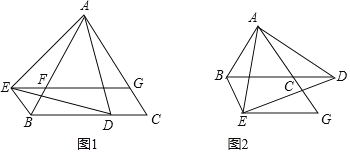
查看答案和解析>>【题目】△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,交射线AC于点G,连接BE.
(1)如图1所示,当点D在线段BC上时,求证:四边形BCGE是平行四边形;
(2)如图2所示,当点D在BC的延长线上时,(1)中的结论是否成立?并请说明理由;
(3)当点D运动到什么位置时,四边形BCGE是菱形?并说明理由.
相关试题

