【题目】周末小明和同学们去“绿博园”的枫湖坐船,观赏风景;如图,小明正在A处的小船上,B处小船上的游客发现点A在点B的正西方向上,C处小船上的游客发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120米.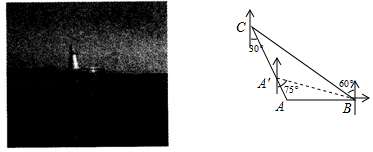
(1)求出此时点A到点C的距离;
(2)若小明从A处沿AC方向向C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时小明所乘坐的小船走的距离.(注:结果保留根号)
参考答案:
【答案】
(1)
解:作CD⊥BA交BA的延长线于点D,
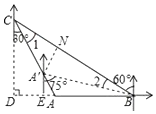
由题意可得,BC=120米,∠CBD=30°,
则CD=60米,
∵∠DCA=30°,
∴AC= ![]() 米,
米,
即此时点A到点C的距离是40 ![]() 米;
米;
(2)
解:作A′N⊥BC于点N,作A′E⊥BA交BA的延长线于点E,

由题意可得,
∠1=30°,∠EA′B=′75°,∠EA′A=30°,∠CBD=30°,
则∠AA′B=45°,
∴∠2=15°,
∴∠A′BE=15°,
∴A′N=A′E,
设AA′=x,
则A′E= ![]() ,
,
∴A′N= ![]() ,
,
∴CA′= ![]() ,
,
∵CA= ![]() ,
,
∴x+ ![]() x=40
x=40 ![]() ,
,
得x= ![]()
答:此时小明所乘坐的小船走的距离是( ![]() )米.
)米.
【解析】(1)根据题意作出合适的辅助线,然后根据锐角三角函数即可求得AC的长;(2)根据题意和锐角三角函数可以求得小明所乘坐的小船走的距离.
【考点精析】本题主要考查了关于方向角问题的相关知识点,需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“A(植物园),B(花卉园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.

请解答下列问题:
(1)本次调查的样本容量是;
(2)补全条形统计图;
(3)若该学校共有3600名学生,试估计该校最想去湿地公园的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.

(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣ ,求⊙O的半径和BF的长.
,求⊙O的半径和BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游商品经销店欲购进A、B两种纪念品,若用380元购进A种纪念品7件,B种纪念品8件;也可以用380元购进A种纪念品10件,B种纪念品6件.
(1)求A、B两种纪念品的进价分别为多少?
(2)若该商店每销售1件A种纪念品可获利5元,每销售1件B种纪念品可获利7元,该商店准备用不超过900元购进A、B两种纪念品40件,且这两种纪念品全部售出时总获利不低于216元,问应该怎样进货,才能使总获利最大,最大为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L:y=﹣
 x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.(1)点A的坐标:_____;点B的坐标:_____;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)在y轴右边,当t为何值时,△NOM≌△AOB,求出此时点M的坐标;
(4)在(3)的条件下,若点G是线段ON上一点,连结MG,△MGN沿MG折叠,点N恰好落在x轴上的点H处,求点G的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生? -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程(组)和不等式(组)
(1)
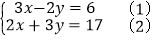 (2)
(2)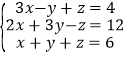
(3)
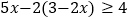 (4)
(4)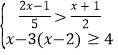
相关试题

