【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,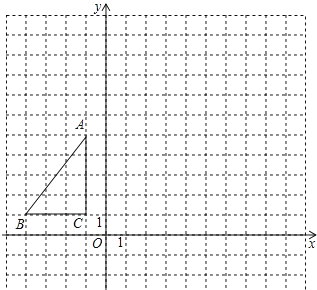
(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
参考答案:
【答案】
(1)解:△AB′C′如图所示

(2)解:点B′的坐标为(3,2),点C′的坐标为(3,5)
(3)解:点C经过的路径为以点A为圆心,AC为半径的圆弧,路径长即为弧长,
∵AC=4,
∴弧长为: ![]() =
= ![]() =2π,
=2π,
即点C经过的路径长为2π
【解析】(1)将△ABC绕点A逆时针旋转90°,得到对应边互相垂直,画出△AB′C′;(2)根据A、B、C的坐标,求出点B′,C′的坐标;(3)根据题意得到点C经过的路径为以点A为圆心,AC为半径的圆弧,路径长即为弧长,根据弧长公式求出点C经过的路径长.
【考点精析】利用弧长计算公式对题目进行判断即可得到答案,需要熟知若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD= .
.
其中正确的结论有( )
A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+
x+ 与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )
与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )
A. 2B. 4C. 6D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别过反比例函数y=
 的图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn)…作x轴的垂线,垂足分别为A1 , A2 , …,An…,连接A1P2 , A2P3 , …,An-1Pn , …,再以A1P1 , A1P2为一组邻边画一个平行四边形A1P1B1P2 , 以A 2P2 , A2P3为一组邻边画一个平行四边形A2P2B2P3 , 点B2的纵坐标是.依此类推,则点Bn的纵坐标是.(结果用含n代数式表示)
的图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn)…作x轴的垂线,垂足分别为A1 , A2 , …,An…,连接A1P2 , A2P3 , …,An-1Pn , …,再以A1P1 , A1P2为一组邻边画一个平行四边形A1P1B1P2 , 以A 2P2 , A2P3为一组邻边画一个平行四边形A2P2B2P3 , 点B2的纵坐标是.依此类推,则点Bn的纵坐标是.(结果用含n代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.

A.4 B.3 C.2 D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,点
,点 为
为 的中点,点
的中点,点 、
、 分别在
分别在 、
、 上,且
上,且 ,下列结论:①
,下列结论:① 是等腰直角三角形;②
是等腰直角三角形;② ;③
;③ ;④
;④ .其中正确的是( )
.其中正确的是( )
A.①②④B.②③④C.①②③D.①②③④
-
科目: 来源: 题型:
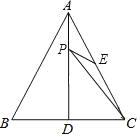
查看答案和解析>>【题目】如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠CPE的度数是_____________.
相关试题

