搜索
【题目】如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，∠A′B′C′可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为（ ）
A. 4
B. 6 C. 3
D. 3
参考答案：
【答案】A
【解析】试题分析：∵在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，
∴∠CAB=30°，故AB=4，
∵△A′B′C可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，
∴AB=A′B′=4，AC=A′C，
∴∠CAA′=∠A′=30°，
∴∠ACB′=∠B′AC=30°，
∴AB′=B′C=2，
∴AA′=2+4=6．
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算（﹣2）100+（﹣2）99的结果是（ ）
A.2
B.﹣2
C.﹣299
D.299 -
科目： 来源： 题型：
查看答案和解析>>【题目】若M=（x﹣3）（x﹣5），N=（x﹣2）（x﹣6），则M与N的大小关系为 ．
-
科目： 来源： 题型：
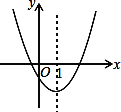
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象的一部分，对称轴是直线x=1．
①b2＞4ac； ②4a-2b+c＜0； ③不等式ax2+bx+c＞0的解集是x≥3.5； ④若（-2，y1），（5，y2）是抛物线上的两点，则y1＜y2．
上述4个判断中，正确的是（ ）
A. ①② B. ①④ C. ①③④ D. ②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】若a＞b，且c为任意有理数，则下列不等式正确的是（ ）
A.ac＞bcB.ac＜bcC.ac2＞bc2D.a+c＞b+c
-
科目： 来源： 题型：
查看答案和解析>>【题目】因式分解：x2-4=__________
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC=2,BC=2
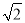,∠A=90°.取一块含45°角的直角三角尺,将直角顶点放在斜边BC的中点O处,一条直角边过点A(如图1).三角尺绕点O顺时针方向旋转,使90°角的两边与Rt△ABC的两边AB,AC分别相交于点E,F(如图2).设BE=x,CF=y.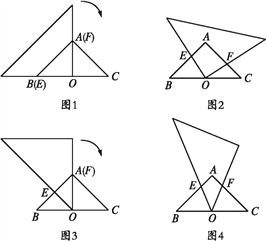
(1)探究:在图2中,线段AE与CF有怎样的大小关系?证明你的结论.
(2)求在上述旋转过程中y与x的函数表达式,并写出x的取值范围.
(3)若将直角三角尺45°角的顶点放在斜边BC边的中点O处,一条直角边过点A(如图3).三角尺绕O点顺时针方向旋转,使45°角的两边与Rt△ABC的两边AB,AC分别相交于点E,F(如图4).在三角尺绕点O旋转的过程中,△OEF是否能成为等腰三角形?若能,直接写出△OEF为等腰三角形时x的值;若不能,请说明理由.
相关试题
