【题目】已知二次函数y=x2﹣2x+m的图象与x轴交于A,B两点,若点A坐标为(﹣1,0),则点B的坐标为_____.
参考答案:
【答案】(3,0).
【解析】
根据二次函数y=x2﹣2x+m的图象与x轴交于A,B两点,点A坐标为(﹣1,0),可以求得m的值,从而可以得到该函数的解析式,进而求得点B的坐标.
∵二次函数y=x2﹣2x+m的图象与x轴交于A,B两点,点A坐标为(﹣1,0),
∴0=(﹣1)2﹣2×(﹣1)+m,
解得,m=﹣3,
∴y=x2﹣2x﹣3,
当y=0时,0=x2﹣2x﹣3=(x﹣3)(x+1),
解得,x1=3,x2=﹣1,
∴点B的坐标为(3,0),
故答案为:(3,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交
 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D.(1)求证:DC=DP;
(2)若∠CAB=30°,当F是
 的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元一次方程ax-b=0的解是x=3,则函数y=ax-b的图象与x轴的交点坐标是( )
A.(-3,0)
B.(3,0)
C.(a,0)
D.(-b,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】一元一次方程kx+b=0(k,b为常数,k≠0)的解即为函数y=的图象与的交点的坐标;反之函数y=kx+b(k,b为常数,k≠0)的图象与的交点的坐标即为方程kx+b=0的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=-2x+10与x轴的交点坐标是,则方程-2x+10=0的解是.
-
科目: 来源: 题型:
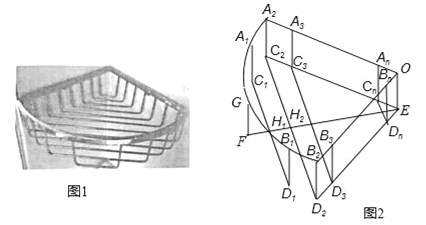
查看答案和解析>>【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在
 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣6)+4的结果是( )
A.-10
B.-2
C.2
D.10
相关试题

